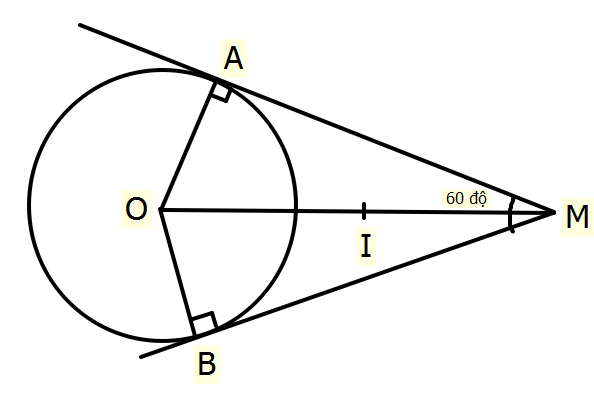
`a)` C/m: `4` điểm `O,A,M,B` thuộc đường tròn
Xét tứ giác `AOBM` có:
`*` `\hat{OAM}=90^o`
`*` `\hat{OBM}=90^o`
(vì `A,B` là tiếp điểm)
`=>` `\hat{OAM}` `+` `\hat{OBM}` `= 90^o +90^o = 180^o`
`=>` Tứ giác `AOBM` nội tiếp đường tròn (tổng hai góc đối nhau `=180^o`)
`=>` `4` điểm `O,A,M,B` cùng thuộc `1` đường tròn
`b)` Tính: `MA,MB` (vì không rõ là đường tròn tâm `O` hay đường tròn có `4` điểm trên nên tớ lấy đường tròn có `4` điểm trên nhé!)
Có tam giác `OAM` vuông tại `A` `=>` Tam giác `OAM` nội tiếp đường tròn, đường kính `OM`
Mà `OAMB` nội tiếp đường tròn `=>` `OAMB` nội tiếp đường tròn, đường kính `OM`
`=>` Tâm của đường tròn này là trung điểm `OM`
Gọi tâm của đường tròn này là `I`
Ta có: `IO=IM=5cm` `=>` `OM=10cm`
Và: `\hat{AMB}=60^o`
Xét tam giác `OMA`, ta có:
`*` `MA=MB` (tính chất hai tiếp tuyến cắt nhau tại `M`)
`*` `\hat{AMO}` `=` `\hat{BMO}` `=` `(\hat{AMB})/2 = (60^o)/2 = 30^o` (`MO` là phân giác của `\hat{AMB}`)
Theo tỉ số lượng giác: `cos\hat{AMO} = (AM)/(OM)`
`=> AM = OM*cos\hat{AMO} = 10 * cos30^o = 5\sqrt{3} cm`
Mà: `MA=MB`
Vậy, `MA=MB = 5\sqrt{3} cm`.













