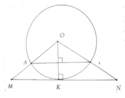
Tiếp tuyến MN, tiếp điểm K. Vì AB//MN
Nên OH ⊥ AB. Tính được OH = 3 5 R. Từ đó tính được KN = 4 3 R => S O M N = 4 3 R 2

Tiếp tuyến MN, tiếp điểm K. Vì AB//MN
Nên OH ⊥ AB. Tính được OH = 3 5 R. Từ đó tính được KN = 4 3 R => S O M N = 4 3 R 2
Cho đường tròn (O; R) và dây AB = 1,6R. Vẽ một tiếp tuyến song song với AB cắt các tia
OA, OB theo thứ tự tại M và N. Tính diện tích tam giác OMN.
Bài 1: Cho (O;R) và dây AB = 1.6R. Vẽ tiếp tuyến song song với AB và cắt OA,OB lần lượt tại M và N. Tính diện tích tam giác MON.
Bài 2: Cho (O); từ điểm M nằm ngoài đường tròn, kẻ 2 cát tuyến tới đường tròn MAD và MBC. Biết MA+MD=MB+MC. Chứng minh AD=BC
Ai trả lời đúng mình tick cho, làm nhanh lên nha, mình đang cần gấp lắm
Thời hạn:12/11/2017
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R. c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC. d) Tính theo R diện tích tam giác BDC.
Cho đường tròn (O; R) đường kính AB. Trên các bán kính OA, OB lần lượt lấy các điểm M và N sao cho OM = ON. Qua M, N vẽ các dây cung CD, EF song song với nhau( C, E thuộc nửa đường tròn đường kính AB).
a) CMR: tứ giác CDFE là hình chữ nhật
b) Cho CM = 2/3 R, góc giữa CD và OA= 60 độ. Tính diện tích tứ giác CDFE
Cho đường tròn ( O;R) , đường kính AB. Trèn bán kính OA , OB lần lượt lấy các điểm M và N sao cho OM = ON . Qua M và N vẽ dây CD và EF song song với nhau ( C , E cùng thuộc một nửa đường tròn đường kính AB ).
a) Chứng minh : Tứ giác CDFE là hình chữ nhật.
b) Cho OA = \(\frac{2}{3}R\), góc nhọn giữa CD và OA = 60 độ . Tính diện tích tứ giác CDFE .
Cho tam giác ABC, đường tròn nội tiếp (I; r). Tiếp tuyến song song vớ. Cho ti BC của (I; r) cắt CA, AB lần lượt tại M,N. Tiếp tuyến song song với CA của (I; r) cắt AB,BC lần lượt tại P,Q. Tiếp tuyến song song với AB của (I; r) cắt BC,CA lần lượt tại R,S. Kí hiệu (I1; r1) và P1, (I2; r2) và P2, (I3; r3) và P3 lần lượt là đường tròn nội tiếp và chu vi của các tam giác AMN,BPQ,CRS; P là chu vi của tam giác ABC. Chứng minh rằng:
1. P1+P2+P3 = P
2. r1+r2+r3 = r.
Cho đường tròn (o;r) và một điểm A nằm cách O một khoảng bằng 2R từ A vẽ các tiếp tuyến AB, AC với đường tròn ( B,C là các tiếp điểm) đường thẳng vuông góc với OB tại O cắt AC tại N, đường thẳng vuông góc với OC tại O cắt AB tại M
a, Tính sinOAB, tanOAB
b,chứng minh OM song song AC ,ON song song AB
c,chứng minh tứ giác AMON là hình thoi từ đó chứng tỏ MN là tiếp tuyến của đường tròn
d, tính diện tích hình thoi AMON
1.Cho tam giác ABC có AD là tia phân giác trong của góc A. Quá D kẻ đường thẳng song song với AB cắt AC ở E và đường thẳng song song với AC cắt AB ở F.
a) Tứ giác AEDF là hình gì? Vì Sao?
b) Đường tròn đường kính AD cắt AB và AC lần lượt tại các điểm M và N. Chứng minh rằng: MN//EF.
2. Cho hai đường tròn (O;R) và(O';R') tiếp xúc trong với nhau tại A, (R>R'). Qua điểm B bất kỳ trên(O') vẽ tiếp tuyến với (O') cắt (O) tại hại điểm M và N, AB cắt (O) tại C. Chứng minh rằng:
a) MN vuông góc với OC
b) AC là tia phân giác của góc MAN