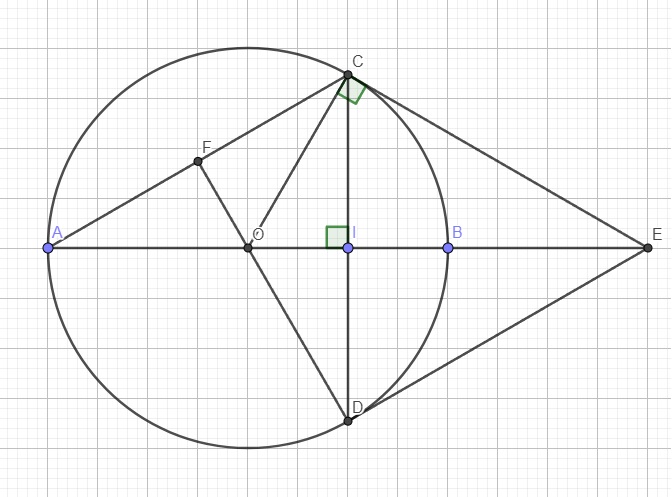
a.
Do EC là tiếp tuyến của (O) tại C \(\Rightarrow EC\perp OC\) hay tam giác OCE vuông tại C
Áp dụng hệ thức lượng trong tam giác vuông OCE với đường cao CI:
\(OC^2=OI.OE\Rightarrow OI.OE=R^2\) (do \(OC=R\))
b.
Do \(AB\perp CD\) tại I nên I là trung điểm CD
\(\Rightarrow OE\) là trung trực của CD
\(\Rightarrow CE=DE\)
Xét hai tam giác OCE và ODE có:
\(\left\{{}\begin{matrix}CE=DE\\OC=OD=R\\OE-chung\end{matrix}\right.\)
\(\Rightarrow\Delta OCE=\Delta ODE\left(c.c.c\right)\) (1) \(\Rightarrow\widehat{ODE}=\widehat{OCE}=90^0\)
\(\Rightarrow ED\perp OD\Rightarrow ED\) là tiếp tuyến của (O)
c.
Do F là trung điểm AC \(\Rightarrow OF\perp AC\) (2)
Trong tam giác vuông OCI: \(cos\widehat{COI}=\dfrac{OI}{OC}=\dfrac{OB}{2OC}=\dfrac{1}{2}\Rightarrow\widehat{COI}=60^0\)
\(\Rightarrow\widehat{CEI}=90^0-\widehat{COI}=30^0\)
\(\widehat{OAC}=\dfrac{180^0-\widehat{AOC}}{2}=\dfrac{180^0-\left(180^0-\widehat{COI}\right)}{2}=30^0\)
\(\Rightarrow\widehat{CEI}=\widehat{OAC}\)
Từ (1) \(\Rightarrow\widehat{DEI}=\widehat{CEI}=30^0\)
\(\Rightarrow\widehat{DEI}=\widehat{OAC}\Rightarrow AC||DE\) (hai góc so le trong bằng nhau)
Mà \(OD\perp DE\) (theo cm câu b) \(\Rightarrow OD\perp AC\) (3)
(2);(3) \(\Rightarrow D,O,F\) thẳng hàng