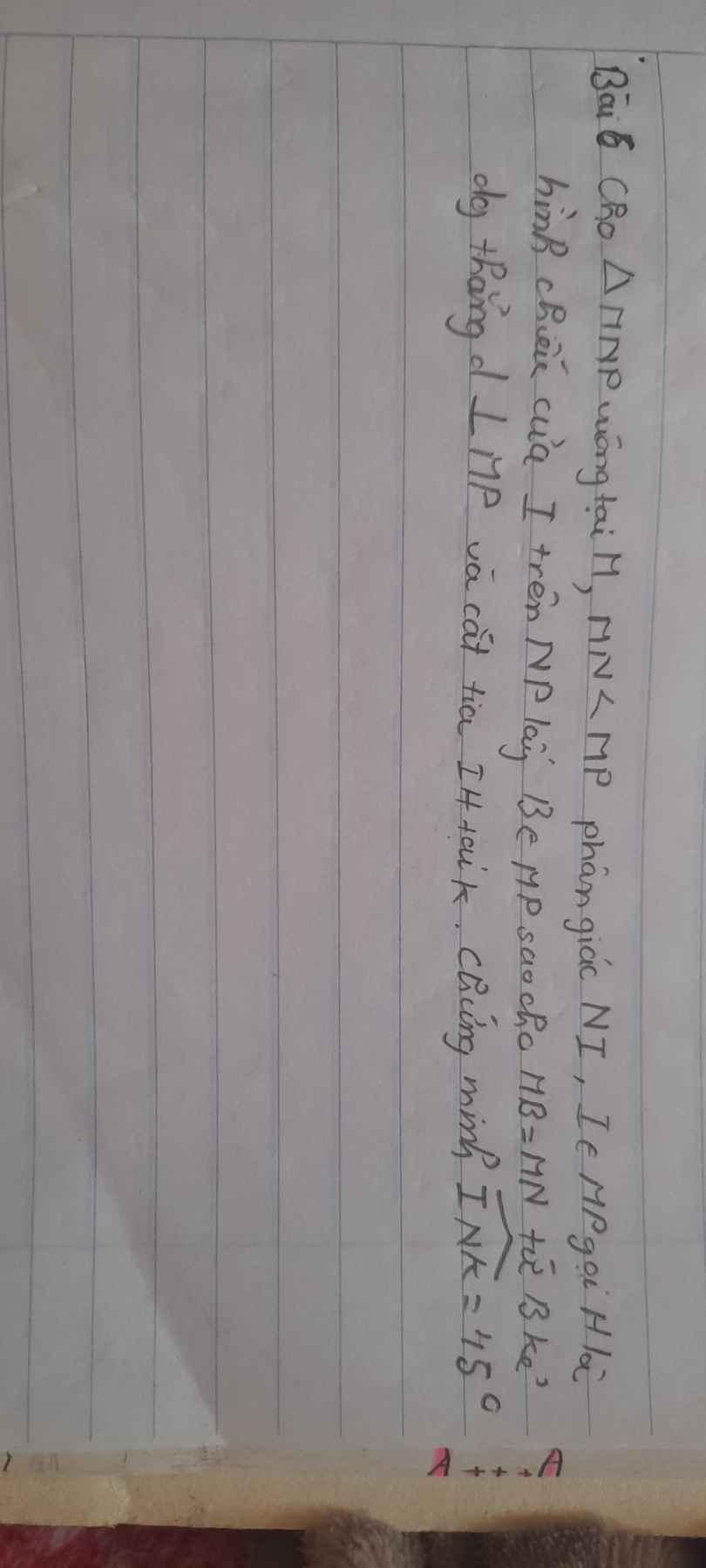Question

Cho ΔMNP có MP>MN, tia phân giác của góc M cắt NP tại D. Gọi I là điểm nằm giữa M và D. Chứng minh MP-MN>IP-IN

Answer 1

Lấy `A` trên `MP` sao cho `MA=MN`

Xét `\triangleMND` và `\triangleMAD` có:

`MN=MA`

`\hat{NMD}=\hat{AMD}`

`MD` cạnh chung

`=>\triangleMND=\triangleMAD(c.g.c)`

`=>ND=AD`

Áp dụng bất đẳng thức trong `\triangleNID` có:

`IN<ID+ND`       `(1)`

Áp dụng bất đẳng thức trong `\triangleIDP` có:

`IP<ID+DP`       `(2)`

Áp dụng bất đẳng thức trong `\triangleADP` có:

`DP-DA<AP`

Từ `(1),(2)=>IP-IN<ID+DP-ID-ND=DP-ND=DP-DA`

`=>IP-IN<AP=MP-MA=MP-MN`

`=>MP-MN>IP-IN`       `(đpcm)`