Cho ΔDEF vuông tại D, DE = 12 cm, DF = 16 cm. Đường phân giác của góc E cắt DF tại M. Kẻ MH vuông góc với EF (H ∈ EF)
a) Vẽ hình
b) So sánh ED và EM
c) So sánh \(\widehat{DEF}\) và \(\widehat{DFE}\)
d) Kẻ DN vuông góc với EF tại N. C/m DH là đường phân giác của \(\widehat{NDF}\)
e) Trên tia đối tia của tia DE lấy điểm I sao cho DI = HF. Gọi K là trung điểm của IF. C/m ba điểm E,M,K thẳng hàng.
f) C/m 3 đường thẳng DE, HM, FK đồng quy.
a: 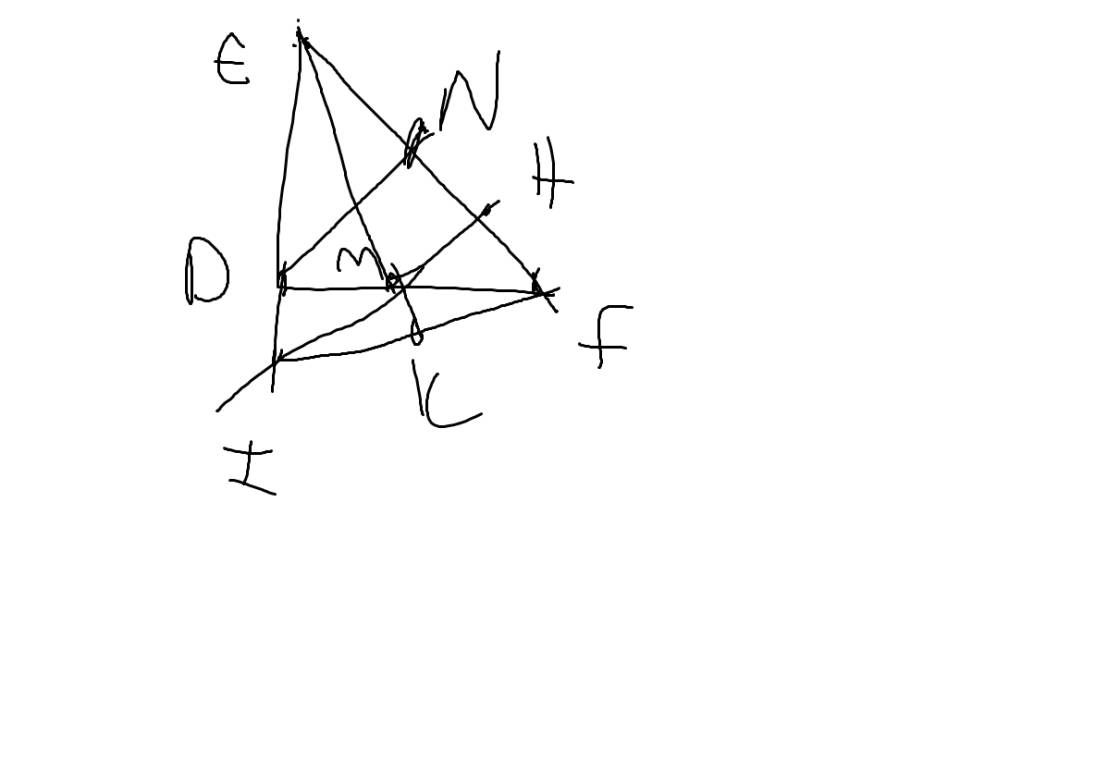
b: Ta có: ΔEDM vuông tại D
=>EM là cạnh lớn nhất trong ΔEDM
=>ED<EM
c: Xét ΔDEF có DE<DF
mà \(\widehat{DFE};\widehat{DEF}\) lần lượt là góc đối diện của các cạnh DE,DF
nên \(\widehat{DFE}< \widehat{DEF}\)
d: Xét ΔEDM vuông tại D và ΔEHM vuông tại H có
EM chung
\(\widehat{DEM}=\widehat{HEM}\)
Do đó: ΔEDM=ΔEHM
=>ED=EH và MD=MH
ta có: ED=EH
=>ΔEDH cân tại E
ta có: \(\widehat{FDH}+\widehat{EDH}=\widehat{EDF}=90^0\)
\(\widehat{NDH}+\widehat{EHD}=90^0\)(ΔNDH vuông tại N)
mà \(\widehat{EDH}=\widehat{EHD}\)(ΔEDH cân tại E)
nên \(\widehat{FDH}=\widehat{NDH}\)
=>DH là phân giác của góc NDF
e: ta có: ED+DI=EI
EH+HF=EF
mà ED=EH và DI=HF
nên EI=EF
=>ΔEIF cân tại E
Ta có: ΔEIF cân tại E
mà EK là đường trung tuyến
nên EK là phân giác của góc IEF
mà EM là phân giác của góc IEF
và EK,EM có điểm chung là E
nên E,K,M thẳng hàng
f: Xét ΔMDI vuông tại D và ΔMHF vuông tại H có
MD=MH
DI=HF
Do đó: ΔMDI=ΔMHF
=>\(\widehat{DMI}=\widehat{HMF}\)
mà \(\widehat{HMF}+\widehat{HMD}=180^0\)(hai góc kề bù)
nên \(\widehat{DMI}+\widehat{HMD}=180^0\)
=>I,M,H thẳng hàng
=>DE,HM,FK đồng quy














