Question

cho ΔABC vuông tại A,đường cao AH biết AH =3cm, BH=4cm

a,tính AB,AC và góc B,C

b,từ H kẻ HE vuông AB ,HF vuông AC.hỏi tứ giác AEHF là hình gì tính EF

c,chứng minh AB x AE=AC x AF

VẼ HÌNH GIÚP MÌNH VS Ạ

Answer 1

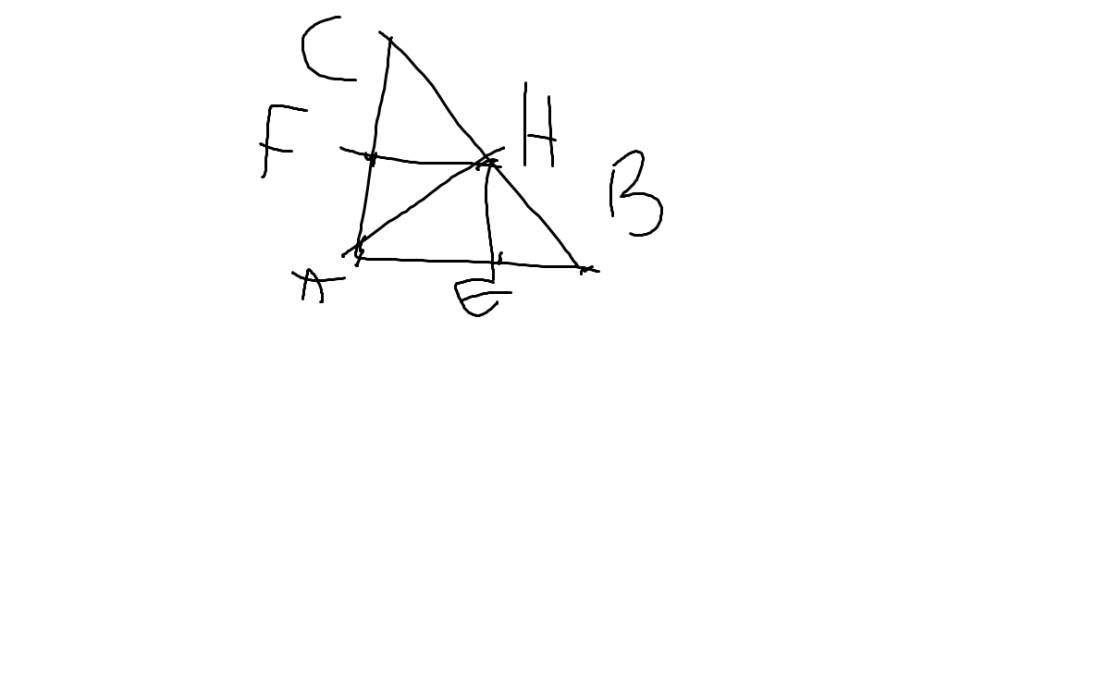
a: ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC\)

=>HC*4=3^2=9

=>HC=2,25(cm)

BC=BH+CH

=2,25+4

=6,25(cm)

XétΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}AB^2=2,25\cdot6,25\\AC^2=4\cdot6,25\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}AB=\sqrt{2,25\cdot6,25}=3,75\left(cm\right)\\AC=\sqrt{25}=5\left(cm\right)\end{matrix}\right.\)

Xét ΔABC vuông tại A có

\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)

nên \(\widehat{C}\simeq37^0\)

=>\(\widehat{B}=90^0-37^0=53^0\)

b: Xét tứ giác AEHF có

\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)

=>AEHF là hình chữ nhật

=>HA=EF=3(cm)

c: ΔAHB vuông tại H có HE là đường cao

nên \(AE\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HF là đường cao

nên \(AF\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)