Question

Cho ΔABC vuông tại A có AB<AC. Kẻ đường cao AH, phân giác AM, kẻ ME⊥AB, MF⊥AC.

a) CMR: BE.BA=BH.BM, HE là tia phân giác góc AHB

b) CM:\(\dfrac{BE}{CF}=\dfrac{HB}{HC}\)

Answer 1

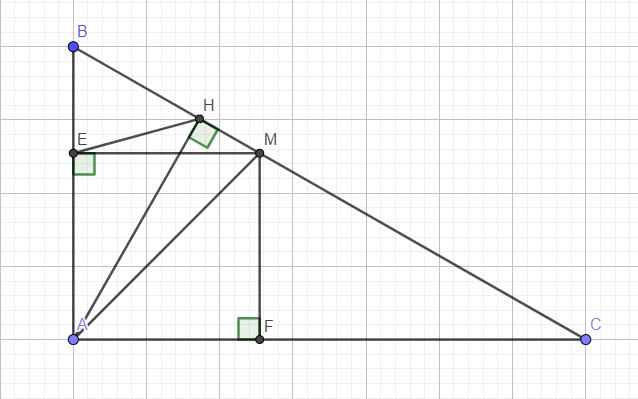
a: Xét ΔBEM vuông tại E và ΔBHA vuông tại H có 

\(\widehat{B}\) chung

Do đó: ΔBEM∼ΔBHA

Suy ra: \(\dfrac{BE}{BH}=\dfrac{BM}{BA}\)

hay \(BE\cdot BA=BH\cdot BM\)

Answer 2

Tứ giác AEHM nội tiếp (E và H cùng nhìn AM dưới 1 góc vuông)

\(\Rightarrow\widehat{AHE}=\widehat{AME}=45^0\) (AEMF là hv nên AME=45 độ)

\(\Rightarrow\widehat{BHE}=\widehat{AHB}-\widehat{AHE}=45^0=\widehat{AHE}\)

\(\Rightarrow HE\) là phân giác AHB

Cũng do AEHM nội tiếp \(\Rightarrow\widehat{EAH}=\widehat{EMH}\)

Mà \(\widehat{EMH}=\widehat{FCH}\) (đồng vị) \(\Rightarrow\widehat{EAH}=\widehat{FCH}\) (1)

Tứ giác AHMF nội tiếp (H và F cùng nhìn AM dưới 1 góc vuông)

\(\Rightarrow\widehat{MHF}=\widehat{MAF}=45^0\Rightarrow\widehat{MHF}=\widehat{AHE}\)  (2)

(1);(2) \(\Rightarrow\Delta AEH\sim\Delta CFH\left(g.g\right)\)

\(\Rightarrow\dfrac{AH}{AE}=\dfrac{CH}{CF}\) (3)

Áp dụng định lý phân giác cho tam giác ABH: \(\dfrac{AH}{AE}=\dfrac{BH}{BE}\) (4)

(3);(4) \(\Rightarrow\dfrac{CH}{CF}=\dfrac{BH}{BE}\Rightarrow\dfrac{BE}{CF}=\dfrac{BH}{CH}\)

Answer 3

Answer 4

Cách 2:

Áp dụng hệ thức lượng: \(AH^2=BH.CH\Rightarrow\dfrac{BH}{CH}=\dfrac{AH^2}{CH^2}\)

Mặt khác hai tam giác vuông ABC và HAC đồng dạng \(\Rightarrow\dfrac{AH}{CH}=\dfrac{AB}{AC}\Rightarrow\dfrac{BH}{CH}=\left(\dfrac{AB}{AC}\right)^2\) (1)

Hai tam giác vuông BEM và MFC đồng dạng (hai góc M và C đồng vị)

\(\Rightarrow\dfrac{BE}{EM}=\dfrac{MF}{CF}\Rightarrow\dfrac{BE}{MF}=\dfrac{MF}{CF}\) (do AEMF là hv nên \(EM=MF\))

\(\Rightarrow BE=\dfrac{MF^2}{CF}\Rightarrow\dfrac{BE}{CF}=\left(\dfrac{MF}{CF}\right)^2\) (2)

Hai tam giác vuông ABC và FMC đồng dạng (chung góc C)

\(\Rightarrow\dfrac{AB}{AC}=\dfrac{MF}{CF}\) (3)

(1);(2);(3) \(\Rightarrow\dfrac{BE}{CF}=\dfrac{HB}{HC}\)