Question

cho ΔABC vuông ở A,đường cao AH.Kẻ HE vuông góc với AB tại E và HF vuông góc với AC tại F
a)CM:tứ giác AFHE là hình chữ nhật
b)Trên tia đối của tia FH lấy điểm M sao cho FH=FM.Trên tia đối của tia EH lấy điểm N sao cho EH=EN.Chứng minh tứ giác AEFM là hình bình hành c)chứng minh A M N thẳng hàng

Answer 1

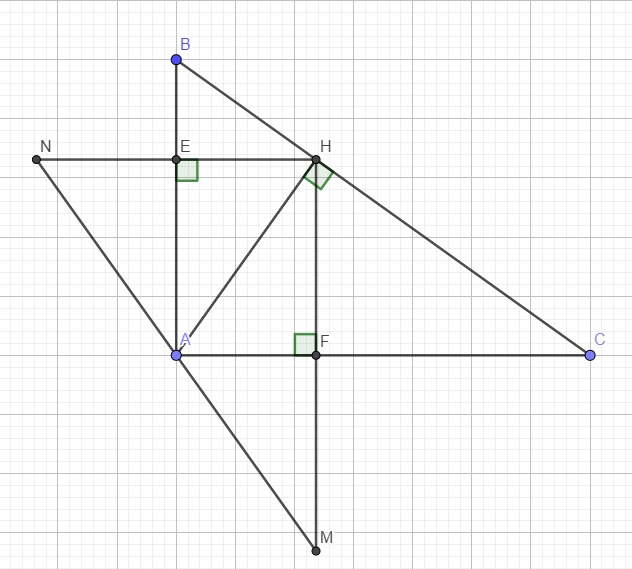
a. 

Xét tứ giác AFHE có:

\(HE||AF\) (cùng vuông góc AB)

\(HF||AE\) (cùng vuông góc AC)

\(\Rightarrow AFHE\) là hình bình hành (tứ giác có 2 cặp cạnh đối song song)

Mà \(\widehat{A}=90^0\left(gt\right)\Rightarrow AFHE\) là hcn (hbh có 1 góc vuông)

b.

Do AFHE là hcn \(\Rightarrow AE=HF\)

Mà \(FH=FM\Rightarrow AE=FM\)

Cũng do \(AFHE\) là hcn \(\Rightarrow AE||HF\Rightarrow AE||FM\) (do F, H, M thẳng hàng)

\(\Rightarrow AEFM\) là hbh (tứ giác có cặp cạnh đối song song và bằng nhau)

c.

Chứng minh tương tự câu b ta có ANEF là hình bình hành

\(\Rightarrow EF||AN\) (1)

Theo câu b AEFM là hbh \(\Rightarrow EF||AM\) (2)

(1);(2) \(\Rightarrow A,M,N\) thẳng hàng

Answer 2