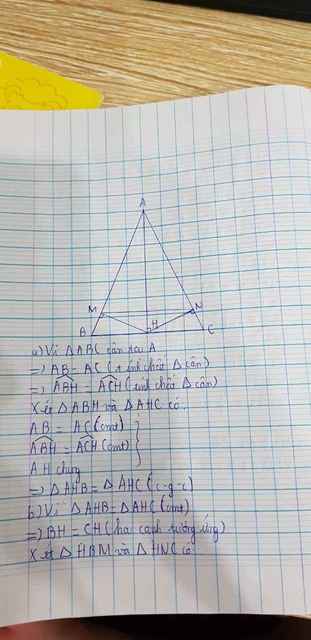a) Xét tam giác AHB vuông tại H và tam giác AHC vuông tại H:
AB = AC (Tam giác ABC cân tại A).
\(\widehat{B}=\widehat{C}\) (Tam giác ABC cân tại A).
\(\Rightarrow\Delta AHB=\Delta AHC\left(ch-gn\right).\)
b) Xét tam giác ABC cân tại A:
AH là đường cao (AH ⊥ BC).
\(\Rightarrow\) AH là đường trung tuyến (T/c tam giác cân).
\(\Rightarrow\) H là trung điểm BC.
Xét tam giác MBH vuông tại M và tam giác NCH vuông tại N:
BH = CH (H là trung điểm BC).
\(\widehat{B}=\widehat{C}\) (Tam giác ABC cân tại A).
\(\Rightarrow\Delta MBH=\Delta NCH\left(ch-gn\right).\\ \Rightarrow BM=CN.\)
Ta có: \(AM=AB-BM;AN=AC-CN.\)
Mà \(\left\{{}\begin{matrix}AB=AC\\BM=CN\end{matrix}\right.\) (cmt).
\(\Rightarrow AM=AN.\Rightarrow\Delta AMN\) cân tại A.
c) Xét tam giác AMN cân tại A:
\(\widehat{AMN}=\dfrac{180^o-\widehat{A}}{2}.\)
Xét tam giác ABC cân tại A:
\(\widehat{ABC}=\dfrac{180^o-\widehat{A}}{2}.\)
\(\Rightarrow\widehat{AMN}=\widehat{ABC}.\\ \Rightarrow MN//BC\left(dhnb\right).\)
a) xét ΔAHB và ΔAHC có:
góc H1=góc H2=90độ
AH chung
góc B=góc C (ΔABC cân tại A)
=> ΔABH=ΔAHC(CH−GN)
=>góc A1=góc A2(2 góc tương ứng)
b) xét ΔAHN và ΔAHM có:
góc M=góc N=90độ
AH chung
góc A1=góc A2(cmt)
=> ΔAHN=ΔAHM(CH−CN)
=> HN = HM (2 cạnh tương ứng)
=> AN = AM (2 cạnh tương ứng)
ΔAMN có: AN = AM (cmt)
=> ΔAMN cân tại A
c) đặt điểm giao nhau giữa AH và MN là K
xét ΔAKM và ΔAKN có:
AK chung
góc A1=góc A2(cmt)
AM = AN (ΔAMN cân tại A)
=> ΔAKM=ΔAKN(c.g.c)
=> góc K1=góc K2
mà 2 góc trên ở vị trí kề bù
=> góc K1=góc K2=90độ
=> MN ⊥AH
mà BC⊥AH
=> MN // BC (tính chất)