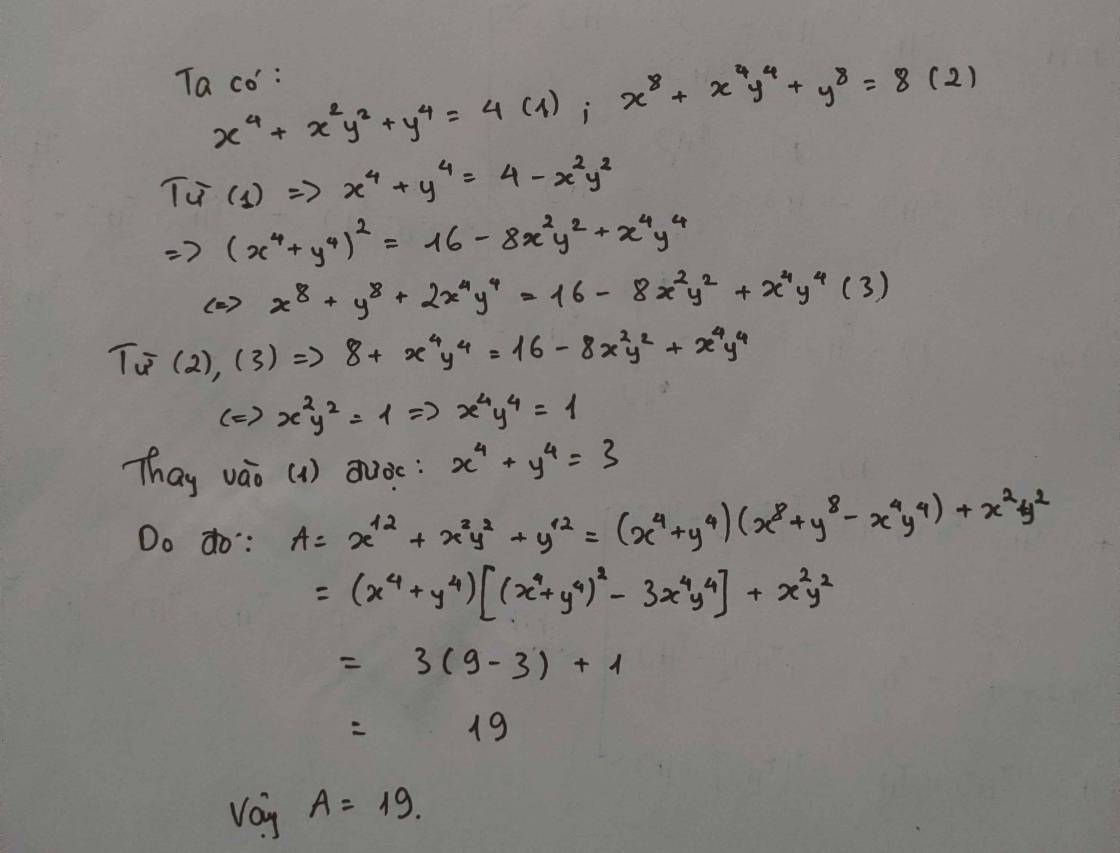Từ x8+x4y4+y8=(x4+y4)2-x4y4=(x4+y4-x2y2) (x4+y4+x2y2)=4(x4+y4-x2y2) =8
=>(x4+y4-x2y2)=2=>x4+y4=2+x2y2 kết hợp với x4+y4+x2y2=4
=> 2+x2y2+x2y2=4 => x2y2=1 (x4y4 sẽ = 1 nốt ) => x4+y4=3 và x8+y8=7
Xét (x4+y4)3=x12+y12+3x4y4(x4+y4)=x12+y12+3.1.3=33=27
=>x12+y12=18=> A = 18+1=19
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Bài 4:Cho các số x,y thoả mãn đẳng thức 5x2+5y2+8xy-2x+2y+2=0
Tính giá trị của biểu thức:M=(x+y)2019 + (x-2)2020 + (y+1)2021
Cho x, y thỏa mãn \(\hept{\begin{cases}x^4+x^2y^2+y^4=4\\x^8+x^4y^4+y^8=8\end{cases}}\)
Tính A = \(x^{12}+x^2y^2+y^{12}\)
Cho x, y thỏa mãn
\(x^4+x^2y^2+y^4=4\)
\(x^8+x^4y^4+y^8=8\)
Tính A = \(x^{12}+x^2y^2+y^{12}\)
Cho các số x,y,z thỏa mãn x4+x2y+y4=4 và x8+x4y4+y+8=8. tính giá trị biểu thức x12+ x2y2 + y12
a)Cho x và y là hai số thực thoã mãn 3x-=1 chứng minh rằng : 5^2-^2<5/4
b)Cho x khác y ; x khác -y;y khác 0 thoã mãn y/x+y + 2y^2/x^2+y^2 + 4y^4/x^4+y^4 + 8y^8/x^8-y^8=2021 tính giá trị x/y
cho các số x,y thoả mãn đẳng thức 5x^2 + 5y^2 +8xy -2x +2y+2=0 tính giá trị các biểu thức M=(x+y)^2017 + (x-2)^2008 +(y+1)^2009
Tính giá trị biểu thức:a) [
12
(
2
x
+
3
y
)
3
-
18
(
2
x
+
3
y
)
2
]:(-6x -...
Đọc tiếp
Tính giá trị biểu thức:
a) [ 12 ( 2 x + 3 y ) 3 - 18 ( 2 x + 3 y ) 2 ]:(-6x - 9y) tại x = 3 2 ;y = l;
b) [ ( 2 x - y ) 4 + 8 ( y - 2 x ) 2 - 2x + y]: (2y - 4x) tại x = 1; y = -2.
cho các số x;y;z thỏa mãn đẳng thức
\(|x+y+z|=4xy+4y+4x^2-2y^2-4\)
tính gá trị bt \(P=\left(x-1\right)^8+\left(y-1\right)^3+\left(z+1\right)^{2019}\)
Tính giá trị nhỏ nhất của A 3(x2 + y2 ) biết x2 + y 2 xy+12Cho các số x,y thỏa mãn đẳng thức x4 + x2y2 + y4 4: x8 +x4y4 + y8 8. Hãy tính giá trị biểu thức A x12 +x2y2 +x12Phân tích đa thức thành nhân tử:a) P ( x2 -x-2)2 + (x-2)2b) Q 6x5+15x4+20x3+15x2+6x+1
Đọc tiếp
Tính giá trị nhỏ nhất của A= 3(x2 + y2 ) biết x2 + y 2 = xy+12Cho các số x,y thỏa mãn đẳng thức x4 + x2y2 + y4 = 4: x8 +x4y4 + y8 = 8. Hãy tính giá trị biểu thức A = x12 +x2y2 +x12Phân tích đa thức thành nhân tử:
a) P= ( x2 -x-2)2 + (x-2)2
b) Q= 6x5+15x4+20x3+15x2+6x+1