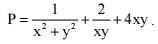Question

Cho các số dương x, y thỏa mãn x + y =1. Tìm giá trị nhỏ nhất của 

Answer 1

\(P=\dfrac{1}{x^2+y^2}+\dfrac{2}{xy}+4xy=\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)+\left(4xy+\dfrac{1}{4xy}\right)+\dfrac{5}{4xy}\)

\(=\left(\dfrac{2xy}{x^2+y^2}+\dfrac{x^2+y^2}{2xy}+2\right)+\left(4xy+\dfrac{1}{4xy}\right)+\dfrac{5}{4xy}\)

+) \(\dfrac{2xy}{x^2+y^2}+\dfrac{x^2+y^2}{2xy}\ge2\)

+) \(4xy+\dfrac{1}{4xy}\ge2\)

+) \(\dfrac{1}{xy}\ge\dfrac{4}{\left(x+y\right)^2}\Leftrightarrow\dfrac{1}{xy}\ge\dfrac{4}{1}\Rightarrow\dfrac{5}{4xy}\ge5\)

\(\Rightarrow minP=11,t\) khi \(x=y=\dfrac{1}{2}\)