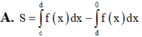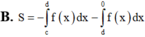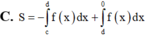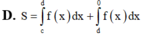Những bài thế này em chỉ cần quan tâm hệ số tự do là đủ:
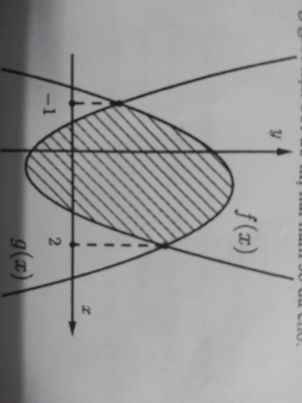
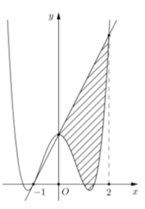
\(f\left(x\right)-g\left(x\right)=0\) có 2 nghiệm -1;2 nên có dạng:
\(f\left(x\right)-g\left(x\right)=k\left(x+1\right)\left(x-2\right)\)
Khai triển biểu thức trên, hệ số tự do ta nhận được là \(-2k\)
Mà \(f\left(x\right)-g\left(x\right)=\left(a-m\right)x^2+\left(b-n\right)x-2\) có hệ số tự do -2
Đồng nhất 2 hệ số tự do \(\Rightarrow-2k=-2\Rightarrow k=1\)
\(\Rightarrow f\left(x\right)-g\left(x\right)=\left(x+1\right)\left(x-2\right)\)
\(\Rightarrow S=\int\limits^2_{-1}\left|f\left(x\right)-g\left(x\right)\right|dx=\int\limits^2_{-1}\left|\left(x+1\right)\left(x-2\right)\right|dx\) bấm máy