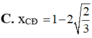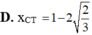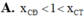Các câu hỏi tương tự
Cho (C) :
y
x
-
1
x
-
2
x
-
log
3
4
có hoành độ điểm cực đại, cực tiểu (xCĐ , xCT) thì : A.
1
x...
Đọc tiếp
Cho (C) : y = x - 1 x - 2 x - log 3 4 có hoành độ điểm cực đại, cực tiểu (xCĐ , xCT) thì :
A. 1 < x C Đ < log 3 4 < x C T < 2
B. 1 < x C Đ < x C T < log 3 4
C. log 3 4 < x C Đ < x C T < 2
D. 1 < x C T < log 3 4 < x C Đ < 2
Hoành độ các điểm cực tiểu của hàm số y = x 4 + 3 x 2 + 2 là:
A. x = −1; B. x = 5;
C. x = 0; D. x = 1, x = 2.
Hoành độ các điểm cực tiểu của hàm số y = x 4 + 3 x 2 + 2 là:
A. x = −1; B. x = 5;
C. x = 0; D. x = 1, x = 2.
Cho hàm số
y
x
4
-
4
x
2
-
1
. Gọi
h
1
,
h
2
lần lượt là khoảng cách từ 2 điểm cực đại và cực tiểu của đồ thị hàm số đến trục hoành. Khi đó tỉ số
h
1
h
2...
Đọc tiếp
Cho hàm số y = x 4 - 4 x 2 - 1 . Gọi h 1 , h 2 lần lượt là khoảng cách từ 2 điểm cực đại và cực tiểu của đồ thị hàm số đến trục hoành. Khi đó tỉ số h 1 h 2 bằng
![]()
![]()
![]()
D. 5
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
(
m
-
1
)
x
+
2
có cực đại, cực tiểu và các đ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Cho hàm số y (m + 2)x3 + 3x2 + mx - 5, m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương A. B. C. D.
Đọc tiếp
Cho hàm số y = (m + 2)x3 + 3x2 + mx - 5, m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương
A. ![]()
B. 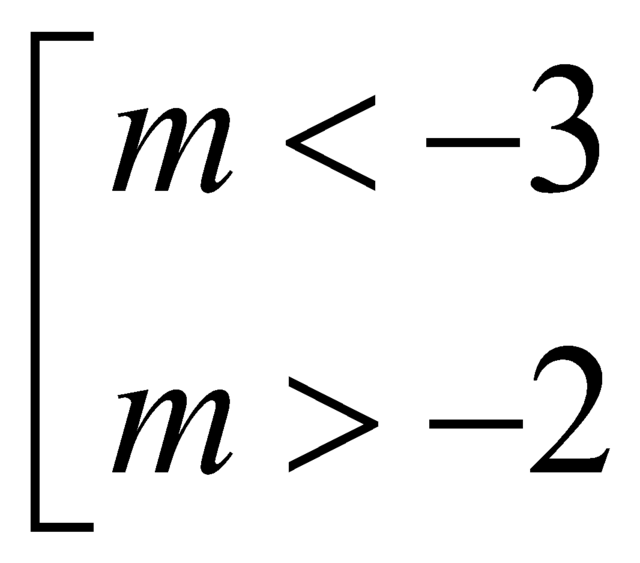
C. ![]()
D. ![]()
Tìm hoành độ các điểm cực đại
x
C
Đ
và hoành độ các điểm cực tiểu
x
C
T
nếu có của đồ thị ycos2x.
Đọc tiếp
Tìm hoành độ các điểm cực đại x C Đ và hoành độ các điểm cực tiểu x C T nếu có của đồ thị y=cos2x.


![]()
![]()
Tìm hoành độ các điểm cực đại
x
C
Đ
; hoành độ các điểm cực tiểu
x
C
T
của đồ thị hàm số ysinx+cosx
Đọc tiếp
Tìm hoành độ các điểm cực đại x C Đ ; hoành độ các điểm cực tiểu x C T của đồ thị hàm số y=sinx+cosx
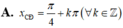
![]()
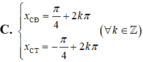
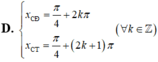
Cho
(
C
)
:
y
2
x
+
x
2
-
2
x
-
1
. Chọn phát biểu đúng về hoành độ điểm cực đại (xCĐ), cực tiểu (xCT).
Đọc tiếp
Cho ( C ) : y = 2 x + x 2 - 2 x - 1 . Chọn phát biểu đúng về hoành độ điểm cực đại (xCĐ), cực tiểu (xCT).
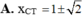
![]()