Các câu hỏi tương tự
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
3
(
m
2
-
1
)
x
-...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Tính tổng tất cả các giá trị thực của tham số m để hàm số y x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng
2
lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O. A. -4 B. -5 C. -6. D. -7
Đọc tiếp
Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
A. -4
B. -5
C. -6.
D. -7
Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y (x + 1)(x – 2)2 A. 5
2
B. 2 C. 2
5
D. 4
Đọc tiếp
Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y = (x + 1)(x – 2)2
A. 5 2
B. 2
C. 2 5
D. 4
Cho hàm số y 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng? A. (x1 – x2)2 8 B. x1x2 2 C. x2 – x1 3 D. x12 + x22 6
Đọc tiếp
Cho hàm số y = 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?
A. (x1 – x2)2 = 8
B. x1x2 = 2
C. x2 – x1 = 3
D. x12 + x22 = 6
Cho hàm số đa thức
f
x
m
x
5
+
n
x
4
+
p
x
3
+
q
x
2
+
h
x
+
r
,
m
,
n
,
p
,
q...
Đọc tiếp
Cho hàm số đa thức f x = m x 5 + n x 4 + p x 3 + q x 2 + h x + r , m , n , p , q , h , r ∈ ℝ . Đồ thị hàm số y = f ' x (như hình vẽ bên dưới) cắt trục hoành tại các điểm có hoành độ lần lượt là -1; 3 2 ; 5 2 ; 11 3 .
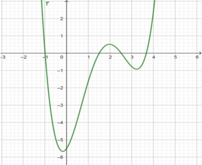
Số điểm cực trị của hàm số g x = f x - m + n + p + q + h + r là
![]()
![]()
![]()
![]()
Cho hàm số y = x mũ 4 trừ 2 m bình x bình + 1 Hỏi có tất cả bao nhiêu số nguyên m để đồ thị hàm số có 2 điểm cực tiểu đều thuộc trục hoành. Giúp minh với
Cho hàm số yx4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất. A. m -1/2 B. m 1/2 C. m2 D. m1
Đọc tiếp
Cho hàm số y=x4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A. m= -1/2
B. m= 1/2
C. m=2
D. m=1
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
(
m
-
1
)
x
+
2
có cực đại, cực tiểu và các đ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Cho hàm số yf(x) xác định và liên tục trên toàn trục số, hàm số f(x) có một điểm cực đại, một điểm cực tiểu với
f
C
Đ
3
;
f
C
T
1
. Biết
l
i
m
x
→
-
∞...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên toàn trục số, hàm số f(x) có một điểm cực đại, một điểm cực tiểu với f C Đ = 3 ; f C T = 1 . Biết l i m x → - ∞ f ( x ) = - ∞ ; l i m x → + ∞ = + ∞ . Hỏi đồ thị (C) cắt trục hoành tại mấy điểm?
![]()
![]()
![]()
![]()





