Các câu hỏi tương tự
Tìm hoành độ các điểm cực đại
x
C
Đ
; hoành độ các điểm cực tiểu
x
C
T
của đồ thị hàm số ysinx+cosx
Đọc tiếp
Tìm hoành độ các điểm cực đại x C Đ ; hoành độ các điểm cực tiểu x C T của đồ thị hàm số y=sinx+cosx
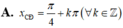
![]()
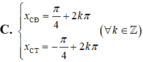
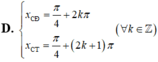
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
(
m
-
1
)
x
+
2
có cực đại, cực tiểu và các đ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Đồ thị hàm số
y
x
2
+
m
x
-
2
m
x
-
1
có các điểm cực đại, cực tiểu có hoành độ dương khi m thỏa mãn: A. m 2 B. 0 m 2 C. -2 m 0 D. 0 m 1
Đọc tiếp
Đồ thị hàm số y = x 2 + m x - 2 m x - 1 có các điểm cực đại, cực tiểu có hoành độ dương khi m thỏa mãn:
A. m > 2
B. 0 < m < 2
C. -2 < m < 0
D. 0 < m < 1
Cho hàm số y (m + 2)x3 + 3x2 + mx - 5, m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương A. B. C. D.
Đọc tiếp
Cho hàm số y = (m + 2)x3 + 3x2 + mx - 5, m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương
A. ![]()
B. 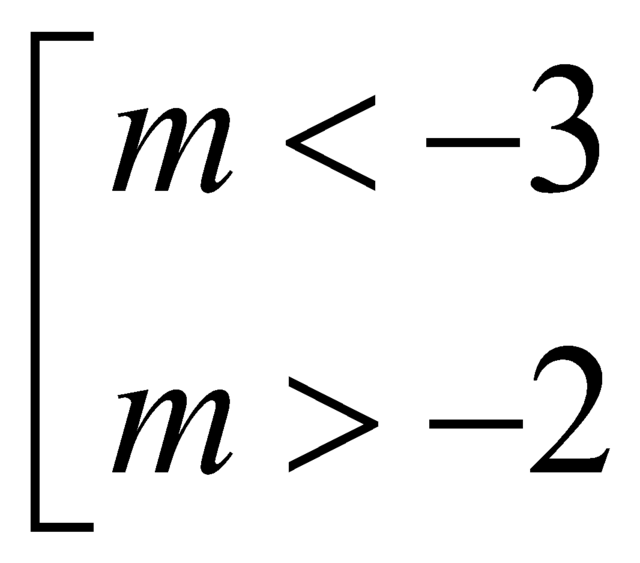
C. ![]()
D. ![]()
Cho hàm số yx3+3x2+mx+m-2 với m là tham số thực, có đồ thị là (C) . Tìm tất cả các giá trị của m để (C) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành. A. m2 B. m
≤
3
C. m3 D.
m
≤
2
.
Đọc tiếp
Cho hàm số y=x3+3x2+mx+m-2 với m là tham số thực, có đồ thị là (C) . Tìm tất cả các giá trị của m để (C) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.
A. m<2
B. m ≤ 3
C. m<3
D. m ≤ 2 .
Tìm hoành độ một điểm cực đại của đồ thị (C):
y
x
2
-
3
4
-
1
.
Đọc tiếp
Tìm hoành độ một điểm cực đại của đồ thị (C): y = x 2 - 3 4 - 1 .
![]()
![]()
![]()
![]()
Cho
(
C
)
:
y
x
2
+
5
x
-
1
. Gọi là hoành độ các điểm cực tiểu, cực đại của (C). Khi đó
Đọc tiếp
Cho ( C ) : y = x 2 + 5 x - 1 . Gọi là hoành độ các điểm cực tiểu, cực đại của (C). Khi đó
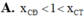
![]()
![]()
![]()
Cho (C) :
y
x
-
1
x
-
2
x
-
log
3
4
có hoành độ điểm cực đại, cực tiểu (xCĐ , xCT) thì : A.
1
x...
Đọc tiếp
Cho (C) : y = x - 1 x - 2 x - log 3 4 có hoành độ điểm cực đại, cực tiểu (xCĐ , xCT) thì :
A. 1 < x C Đ < log 3 4 < x C T < 2
B. 1 < x C Đ < x C T < log 3 4
C. log 3 4 < x C Đ < x C T < 2
D. 1 < x C T < log 3 4 < x C Đ < 2
Cho hàm số yf(x) xác định và liên tục trên toàn trục số, hàm số f(x) có một điểm cực đại, một điểm cực tiểu với
f
C
Đ
3
;
f
C
T
1
. Biết
l
i
m
x
→
-
∞...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên toàn trục số, hàm số f(x) có một điểm cực đại, một điểm cực tiểu với f C Đ = 3 ; f C T = 1 . Biết l i m x → - ∞ f ( x ) = - ∞ ; l i m x → + ∞ = + ∞ . Hỏi đồ thị (C) cắt trục hoành tại mấy điểm?
![]()
![]()
![]()
![]()





