\(a.P=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{2\left(\sqrt{x}+12\right)}{x-9}\right)\cdot\dfrac{\sqrt{x}+5}{\sqrt{x}-8}\\ =\left[\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{2\left(\sqrt{x}+12\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right]\cdot\dfrac{\sqrt{x}+5}{\sqrt{x}-8}\\ =\dfrac{x-3\sqrt{x}-2\sqrt{x}-24}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}+5}{\sqrt{x}-8}\\ =\dfrac{x-5\sqrt{x}-24}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}+5}{\sqrt{x}-8}\\ =\dfrac{\left(\sqrt{x}-8\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}+5}{\sqrt{x}-8}\\ =\dfrac{\sqrt{x}+5}{\sqrt{x}-3}\)
\(b.P\le1=>\dfrac{\sqrt{x}+5}{\sqrt{x}-3}\le1\Leftrightarrow\dfrac{\sqrt{x}+5-\sqrt{x}+3}{\sqrt{x}-3}\le0\\ \Leftrightarrow\dfrac{8}{\sqrt{x}-3}\le0\Leftrightarrow\sqrt{x}-3< 0\\ \Leftrightarrow x< 9\)
Kết hợp với đkxđ: `0≤x<9`
a)
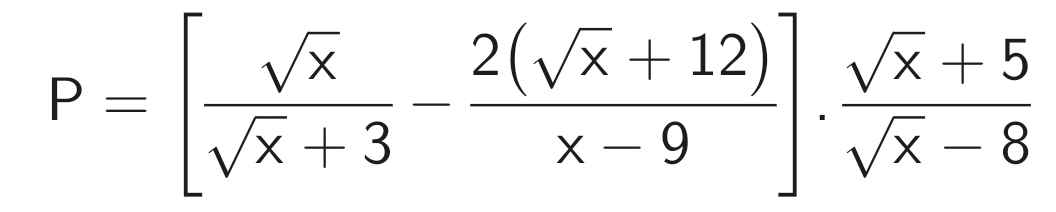
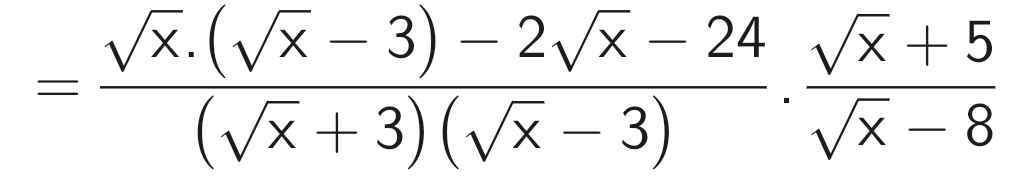
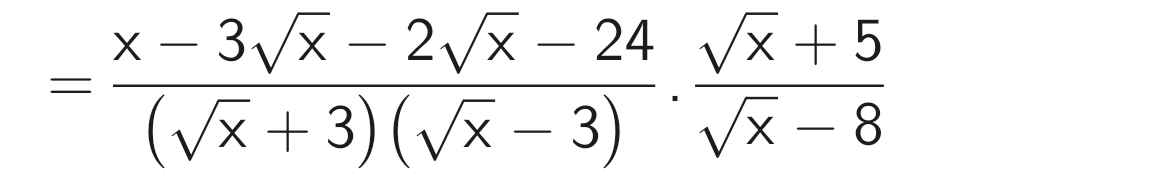
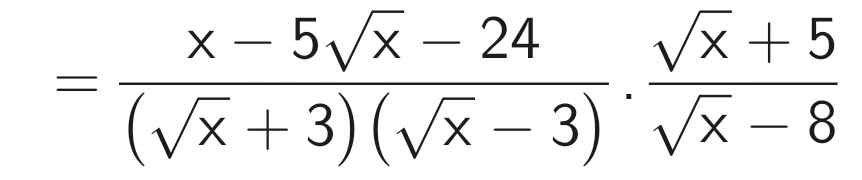
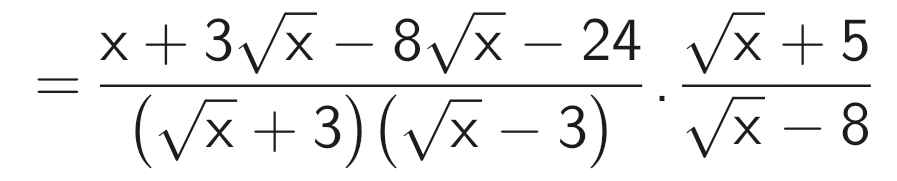
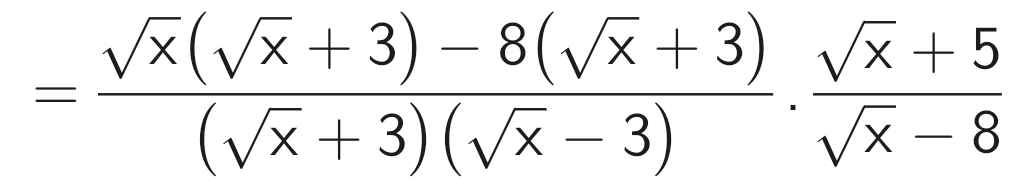
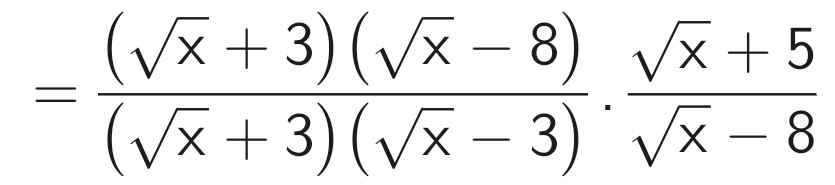

b) P ≤ 1
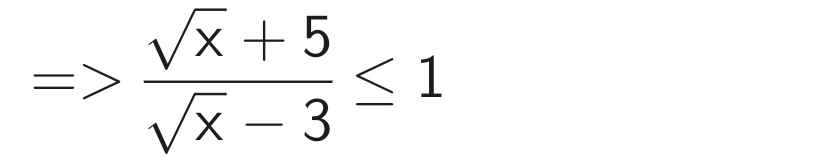
*) Với 0 x < 9, ta có:
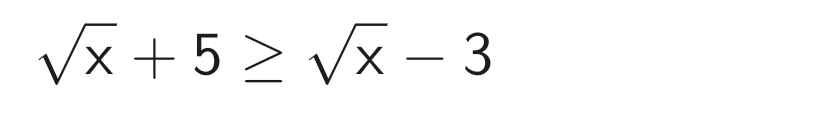
0x ≥ -3 - 5
0x ≥ -8 (luôn đúng)
*) Với x > 9, ta có:
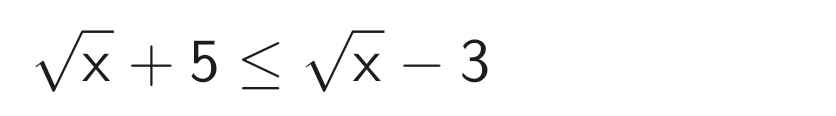
0x ≤ -3 - 5
0x ≤ -8 (vô lý)
Vậy 0 ≤ x < 9 thì P ≤ 1















