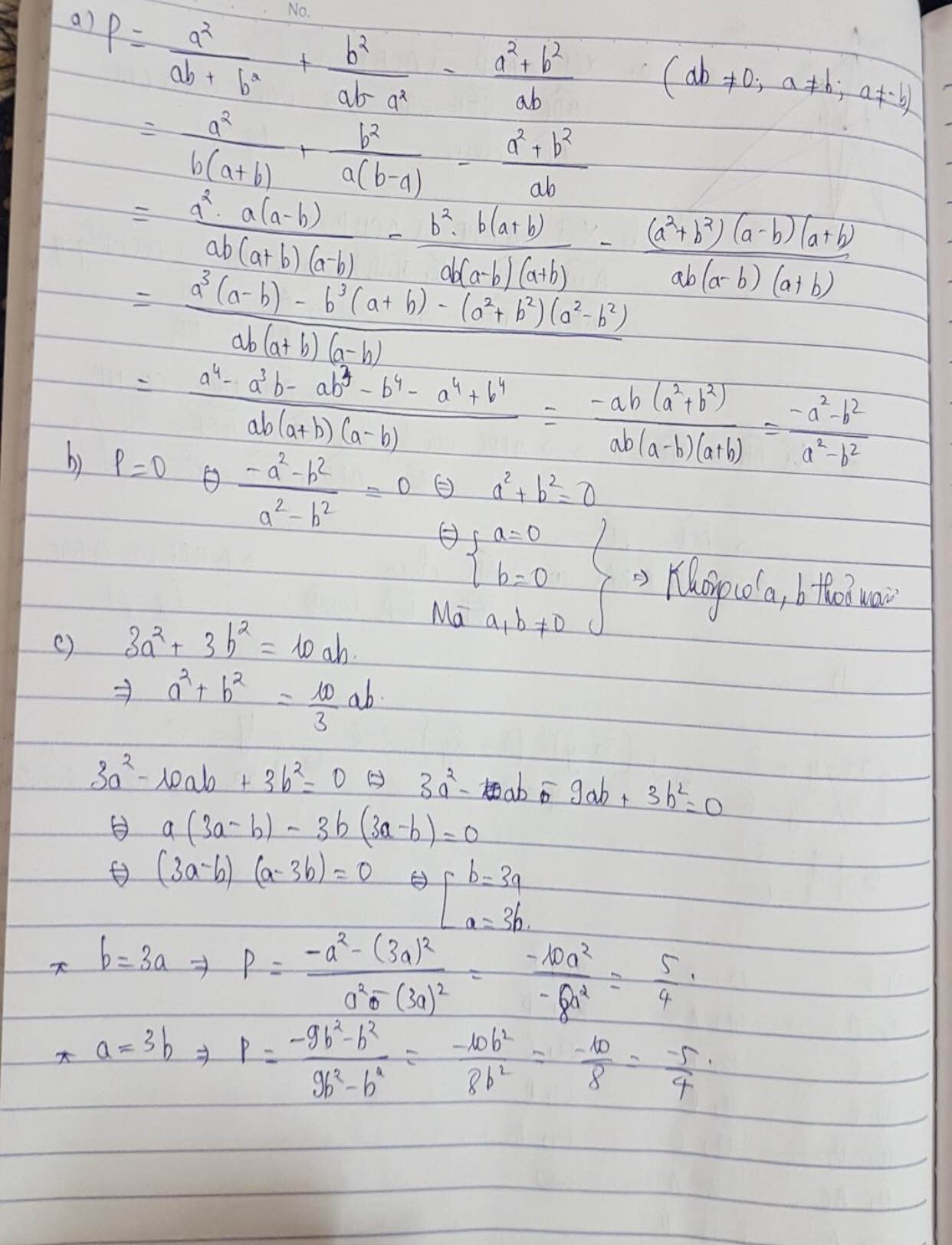\(P=\dfrac{a^2}{ab+b^2}+\dfrac{b^2}{ab-a^2}-\dfrac{a^2+b^2}{ab}\) (\(a\ne b;a\ne0;a\ne-b;b\ne0\))
\(=\dfrac{a^2}{b\left(a+b\right)}+\dfrac{b^2}{a\left(b-a\right)}-\dfrac{a^2+b^2}{ab}\)
\(=\dfrac{a^3\left(a-b\right)-b^3\left(a+b\right)-\left(a^2+b^2\right)\left(a+b\right)\left(a-b\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{a^4-a^3b-b^3a-b^4-\left(a^2+b^2\right)\left(a^2-b^2\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{a^4-a^3b-b^3a-b^4-\left(a^4-b^4\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{-a^3b-b^3a}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{-ab\left(a^2+b^2\right)}{ab\left(a+b\right)\left(a-b\right)}=-\dfrac{a^2+b^2}{a^2-b^2}\).
b) -Ta có: \(P=0\)
\(\Leftrightarrow-\dfrac{a^2+b^2}{a^2-b^2}=0\)
\(\Leftrightarrow a^2+b^2=0\)
-Vì \(a^2\ge0;b^2\ge0\)
\(\Rightarrow a=0;b=0\) (không thỏa mãn điều kiện).
-Vậy không có giá trị nào của a,b để \(P=0\).
c)