a: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
b: \(M=\dfrac{x^2+6x+9-x^2+6x-9-36}{\left(x-3\right)\left(x+3\right)}=\dfrac{12x-36}{\left(x-3\right)\left(x+3\right)}=\dfrac{12}{x+3}\)
c: Thay x=0 vào M, ta được:
M=12/3=4
a: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
b: \(M=\dfrac{x^2+6x+9-x^2+6x-9-36}{\left(x-3\right)\left(x+3\right)}=\dfrac{12x-36}{\left(x-3\right)\left(x+3\right)}=\dfrac{12}{x+3}\)
c: Thay x=0 vào M, ta được:
M=12/3=4
Cho biểu thức .
a.Tìm điều kiện xác định của biểu thức M.
b.Rút gọn biểu thức M
b.Tính giá trị của biểu thức M tại x = 0.
Cho biểu thức .
a.Tìm điều kiện xác định của biểu thức M.
b.Rút gọn biểu thức M
b.Tính giá trị của biểu thức M tại x = 0.
Cho biểu thức .
a.Tìm điều kiện xác định của biểu thức M.
b.Rút gọn biểu thức M
b.Tính giá trị của biểu thức M tại x = 0.
Rút gọn biểu thức: A = a 2 + 2 a 2 a + 10 + a − 5 a + 50 − 5 a 2 a ( a + 5 ) .
a) Tìm điều kiện xác định của biểu thức A;
b) Rút gọn biểu thức;
c) Tính giá trị của biểu thức tại a = -1
d) Tìm giá trị của a để A = 0.
Bài 2: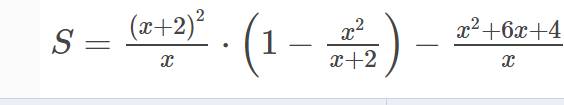
a) tìm điều kiện xác định của biểu thức S
b) Rút gọn rồi tính giá trị của biểu thức S tại x=0;1
c) tìm giá trị lớn nhất của biểu thức S
Cho biểu thức
1 3 1
. 1 1 2
x x x A
x x
1) Tìm điều kiện của x để biểu thức A được xác định. 2) Rút gọn biểu thức A. 3) Tính giá trị của biểu thức A tại x 5. 4) Tìm các giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
Cho biểu thức A=x2-4x+4/5x-10
a) Với điều kiện nào của x thì giá trị biểu thức của A được xác định
b) Rút gọn biểu thức A
c) Tìm giá trị của biểu thức A tại x=-2018
Cho biểu thức
2 1 1
1 . 1
1 1
A x
x x
a) Tìm điều kiện của x để biểu thức A xác định. b) Rút gọn biểu thức A
c) Tính giá trị của A tại x = 3
Cho biểu thức
A = x^2 / (x^2 - 4) - x / (x -2) + 2 / (x+2)
a) Với điều kiện nào của x thì giá trị của biểu thức A được xác định.
b) Rút gọn biểu thức A
c) Tìm giá trị của biểu thức A tại x = 1