\(a^3+b^3+c^3=3abc\)
<=>\(a^3+b^3+c^3-3abc=0\)
<=>\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)(*)
Thay a+b+c=0 vào biểu thức (*) ta có:
\(0.\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)luôn đúng!
Vậy với a+b+c=0 thì a3+b3+c3=3ab (đpcm)
thay a^3+b^3=(a+b)^3 -3ab(a+b) .Ta có :
a^3+b^3+c^3-3abc=0
<=>(a+b)^3 -3ab(a+b) +c^3 - 3abc=0
<=>[(a+b)^3 +c^3] -3ab.(a+b+c)=0
<=>(a+b+c). [(a+b)^2 -c.(a+b)+c^2] -3ab(a+b+c)=0
<=>(a+b+c).(a^2+2ab+b^2-ca-cb+c^2-3ab)...
<=>(a+b+c).(a^2+b^2+c^2-ab-bc-ca)=0
luôn đúng do a+b+c=0
thay a^3+b^3=(a+b)^3 -3ab(a+b) .Ta có :
a^3+b^3+c^3-3abc=0
<=>(a+b)^3 -3ab(a+b) +c^3 - 3abc=0
<=>[(a+b)^3 +c^3] -3ab.(a+b+c)=0
<=>(a+b+c). [(a+b)^2 -c.(a+b)+c^2] -3ab(a+b+c)=0
<=>(a+b+c).(a^2+2ab+b^2-ca-cb+c^2-3ab)...
<=>(a+b+c).(a^2+b^2+c^2-ab-bc-ca)=0
luôn đúng do a+b+c=0
thay a^3+b^3=(a+b)^3 -3ab(a+b) .Ta có :
a^3+b^3+c^3-3abc=0
<=>(a+b)^3 -3ab(a+b) +c^3 - 3abc=0
<=>[(a+b)^3 +c^3] -3ab.(a+b+c)=0
<=>(a+b+c). [(a+b)^2 -c.(a+b)+c^2] -3ab(a+b+c)=0
<=>(a+b+c).(a^2+2ab+b^2-ca-cb+c^2-3ab)...
<=>(a+b+c).(a^2+b^2+c^2-ab-bc-ca)=0
luôn đúng do a+b+c=0
thay a^3+b^3=(a+b)^3 -3ab(a+b) .Ta có :
a^3+b^3+c^3-3abc=0
<=>(a+b)^3 -3ab(a+b) +c^3 - 3abc=0
<=>[(a+b)^3 +c^3] -3ab.(a+b+c)=0
<=>(a+b+c). [(a+b)^2 -c.(a+b)+c^2] -3ab(a+b+c)=0
<=>(a+b+c).(a^2+2ab+b^2-ca-cb+c^2-3ab)...
<=>(a+b+c).(a^2+b^2+c^2-ab-bc-ca)=0
luôn đúng do a+b+c=0
a\(^3\)+b^3+c^3-3abc=0
<=>(a+b)^3 -3ab(a+b) +c^3 - 3abc=0
<=>[(a+b)^3 +c^3] -3ab.(a+b+c)=0
<=>(a+b+c). [(a+b)^2 -c.(a+b)+c^2] -3ab(a+b+c)=0
<=>(a+b+c).(a^2+2ab+b^2-ca-cb+c^2-3ab)...
<=>(a+b+c).(a^2+b^2+c^2-ab-bc-ca)=0
luôn đúng do a+b+c=0
ta có:\(a+b+c=0\)
suy ra:\(a-b=-c\)
\(a^3+b^3+c^3=3abc\)
\(a^3+b^3+b^3-3abc=0\)
\(a^3+b^3+c^3=3abc\)
(=)\(a^3+b^3+c^3-3abc=0\)
(=)(a+b+c) . \((a^2+b^2+c^2-ab-bc-ac)=0\)(*)
thay a+b+c=0 vào biểu thức (*) ta có :
0. \(\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)luôn đúng
vậy với a+b+c=0 thì \(a^3+b^3+c^3=3ab\left(dpcm\right)\)
a+b+c=0
=>(a+b+c)3=0
=>a3+b3+c3+3a2b+3ab2+3b2c+3bc2+3a2c+3ac2+6abc=0
=>a3+b3+c3+(3a2b+3ab2+3abc)+(3b2c+3bc2+3abc)+(3a2c+3ac2+3abc)-3abc=0
=>a3+b3+c3+3ab(a+b+c)+3bc(a+b+c)+3ac(a+b+c)=3abc
Do a+b+c=0
=>a3+b3+c3=3abc(ĐPCM)
Ta có : \(a+b+c=0\)
\(\Rightarrow\hept{\begin{cases}a+b=-c\\b+c=-a\\a+c=-b\end{cases}}\) ( 1 )
Ta có : \(a+b+c=0\)
\(\Rightarrow\left(a+b+c\right)^3=0\)
\(\Rightarrow\left[\left(a+b\right)+c\right]^3=0\)
\(\Rightarrow\left(a+b\right)^3+c^3+3\left(a+b\right)^2c+3\left(a+b\right)c^2=0\)
\(\Rightarrow\left(a+b\right)^3+c^3+3\left(a+b\right)\left[\left(a+b\right)c+c^2\right]=0\)
\(\Rightarrow\left(a+b\right)^3+c^3+3\left(a+b\right)c\left(a+b+c\right)=0\)
\(\Rightarrow a^3+b^3+3a^2b+3ab^2+c^3+3\left(a+b\right)c\left(a+b+c\right)=0\)
\(\Rightarrow a^3+b^3+3ab\left(a+b\right)+c^3+3\left(a+b\right)c\left(a+b+c\right)=0\)
\(\Rightarrow a^3+b^3+c^3+3\left(a+b\right)\left[ab+c\left(a+b+c\right)\right]=0\)
\(\Rightarrow a^3+b^3+c^3+3\left(a+b\right)\left(ab+ca+cb+c^2\right)=0\)
\(\Rightarrow a^3+b^3+c^3+3\left(a+b\right)\left[\left(ab+ca\right)+\left(cb+c^2\right)\right]=0\)
\(\Rightarrow a^3+b^3+c^3+3\left(a+b\right)\left[a\left(b+c\right)+c\left(b+c\right)\right]=0\)
\(\Rightarrow a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(a+c\right)=0\) ( 2 )
Thay ( 1 ) vào ( 2 ) ta được :
\(\Rightarrow a^3+b^3+c^3+3.\left(-c\right).\left(-a\right).\left(-b\right)=0\)
\(\Rightarrow a^3+b^3+c^3-3abc=0\)
\(\Rightarrow a^3+b^3+c^3=3abc\)






















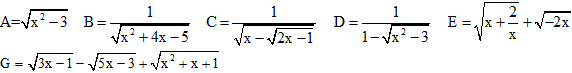 Mn giúp em với ;-;
Mn giúp em với ;-;

