a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
góc A chung
Do đo: ΔABH=ΔACK
Suy ra: BH=CK
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đo: ΔKBC=ΔHCB
Suy ra: KB=HC
a)
xét ΔABH vuông tại H và ΔACK vuông tại K có :
AB = AC
góc A : cạnh chung
=> do đó : ΔABH = ΔACK
=> BH = CK
b)
xét ΔKBC vuông tại K và ΔHCB vuông tại H có :
BC: cạnh chung
KC = HB
=> do đó : ΔKBC = ΔHCB
=> KB = HC
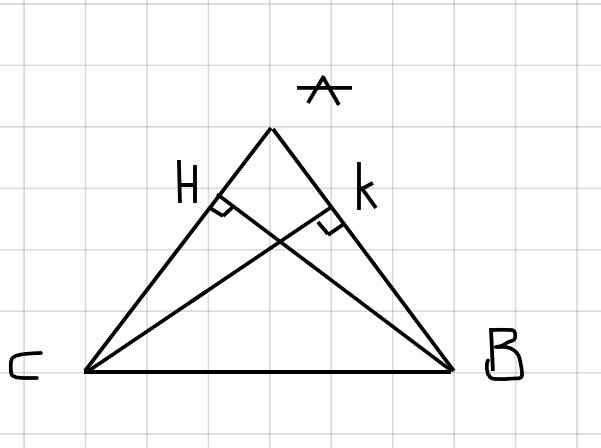
`a.` xét `Δ ACK` vuông tại `K`
`Δ ABH` vuông tại `H` có:
Góc `A` là chung
`AB=AC`
`=>ΔABH=ΔACK(` Cạnh huyền-góc nhọn `)`
`=>BH=CK`
`b.` xét `ΔKBC` vuông tại K
`ΔHCB` vuông tại H có:
`BC` là chung
`BH=CK` (theo câu a)
`=>ΔKBC=ΔHCB(c-g-c)`
`=> KB=HC`
`-`Mong bạn ko chê hình :")

















