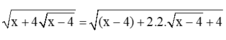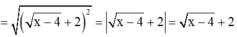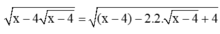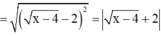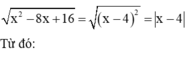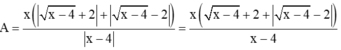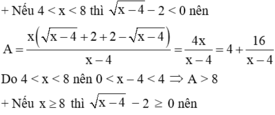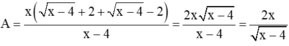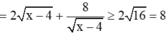Các câu hỏi tương tự
1, tính a/ (3+√5)(√10 - √2)√(3-√5)b/[√2-√(3-√5)].√2c/(√10 + √6).√(8-2√15)2, tìm x biết a/ √(x+5)1+√xb/√x + √(x-1)1c/ √(3-x) + √(x-5)103, phân tích đa thức thành nhân tử:a/ ab+b√a+√a+1 với a ≥0b/ x-2√xy + y với x,y ≥ 0c/√xy + 2√x - 3√y -6 với x,y ≥ 04, chứng minh rằng a/ (4+√15).(√10-√6).√(4-√15)2b/ √a + √b √(a+b) (a,b0)5, Cho √(8-a) + √(5+a) 5 tính √[(8-a).(5+a)]6, rút gọn √(7+2√10)-√15P/s : mn giúp e với nha
Đọc tiếp
1, tính a/ (3+√5)(√10 - √2)√(3-√5)
b/[√2-√(3-√5)].√2
c/(√10 + √6).√(8-2√15)
2, tìm x biết a/ √(x+5)=1+√x
b/√x + √(x-1)=1
c/ √(3-x) + √(x-5)=10
3, phân tích đa thức thành nhân tử:
a/ ab+b√a+√a+1 với a ≥0
b/ x-2√xy + y với x,y ≥ 0
c/√xy + 2√x - 3√y -6 với x,y ≥ 0
4, chứng minh rằng a/ (4+√15).(√10-√6).√(4-√15)=2
b/ √a + √b > √(a+b) (a,b>0)
5, Cho √(8-a) + √(5+a) = 5 tính √[(8-a).(5+a)]
6, rút gọn √(7+2√10)-√15
P/s : mn giúp e với nha
a : \(\dfrac{y}{x}.\sqrt{\dfrac{x^2}{y^4}}\) với y ≥ 0 , y ≠ 0
b : \(\dfrac{5}{2}x^3y^3.\sqrt{\dfrac{16}{x^4y^8}}\)với x,y ≠ 0
c : \(ab^2\sqrt{\dfrac{3}{a^2b^4}}\)với a ≥ 0 , b ≠ 0
a. 3x⁴ - x² - 234 = 0 b. x/1-x = 2x+3/(x-1)(x+2) c. x²(x+1)-3x=3x²-2x-2 d. (x+4)(x+5)(x+7)(x+8)=4
5 tháng 6 2021 lúc 15:55
Cho x,y>0,x+y=1.CM:`A=(x+1/x)^2+(y+1/y)^2>=25/2`
`A=x^2+1/x^2+2+y^2+1/y^2+2`
`=x^2+y^2+1/x^2+1/y^2+4`
`=(x^2+1/(16x^2))+(y^2+1/(16y^2))+4+15/16(1/x^2+1/y^2)`
Áp dụng BĐt cosi và `1/a^2+1/b^2>=8/(a+b)^2`
`=>A>=1/2+1/2+4+15/16(8/(x+y)^2)`
`<=>A>=5+15/2=25/2`
Dấu "=" `<=>x=y=1/2`
Không làm theo cách sau:
Rút gọn
a) a-b/√a-√b (a, b>0;a≠b)
b) x-2√x +1/√x -1(x≥0;x≠1)
c) √4+√7+4√3
Giải pt
a) √x²-4x+4=3
b) √x-5 +√5-x=1
c) √x²-4 -x²+4=0
Tìm x để biểu thức sau có nghĩa
a) √-2x+3
b) 1+x²
c) √-5/x²+6
d) √x/3
e) √2/x²
câu 1 giúp mk với nhé! thanks!a:) cho a,b,c khác 0 và a+b+c 0 tính giá trị của biểu thức:Qfrac{1}{a^2+b^2-c^2}+frac{1}{b^2+c^2-a^2}+frac{1}{a^2+c^2-b^2}b) cho a,b 1 CMR : frac{1}{1+a^2}+frac{1}{1+b^2}gefrac{2}{1+2ab}c) giải hệ phương trìnhhept{begin{cases}sqrt{2x+3}+sqrt{4-y}4sqrt{2y+3}+sqrt{4-x}4end{cases}}d) CMR f(x) x^{99}+x^{88}+x^{77}+...+x^{11}+1chia hết cho g(x)x^9+x^8+x^7+...+x+1
Đọc tiếp
câu 1 giúp mk với nhé! thanks!
a:) cho a,b,c khác 0 và a+b+c = 0 tính giá trị của biểu thức:
Q=\(\frac{1}{a^2+b^2-c^2}+\frac{1}{b^2+c^2-a^2}+\frac{1}{a^2+c^2-b^2}\)
b) cho a,b >= 1 CMR : \(\frac{1}{1+a^2}+\frac{1}{1+b^2}\ge\frac{2}{1+2ab}\)
c) giải hệ phương trình
\(\hept{\begin{cases}\sqrt{2x+3}+\sqrt{4-y}=4\\\sqrt{2y+3}+\sqrt{4-x}=4\end{cases}}\)
d) CMR f(x)= \(x^{99}+x^{88}+x^{77}+...+x^{11}+1\)
chia hết cho g(x)=\(x^9+x^8+x^7+...+x+1\)
16 tháng 8 2015 lúc 6:24
Cho biểu thức: \(A=\frac{\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}}{\sqrt{\frac{16}{x^2}-\frac{8}{x}+1}}\)
a) Với giá trị nào của x thì A xác định.
b) Tìm các giá trị nguyên của x để A có giá trị nguyên.
c) Tim giá trị của x để A đạt GTNN.
28 tháng 8 2021 lúc 21:01
Gpt: x^4-3x^2-10x-40Làm kiểu này được không ạ:ax^4+bx^2+cx+d0
Leftrightarrow x^4+dfrac{b}{a}x^2+dfrac{c}{a}x+dfrac{d}{a}0
Leftrightarrowleft(x^4+2yx^2+y^2right)-2yx^2-y^2+dfrac{b}{a}x^2+dfrac{c}{a}x+dfrac{d}{a}0
Leftrightarrowleft(x^2+2yright)^2+x^2.left(dfrac{b}{a}-2yright)+dfrac{c}{a}x+dfrac{d}{a}-y^20Ta tìm y: x^2.left(dfrac{b}{a}-2yright)+dfrac{c}{a}x+dfrac{d}{a}-y^2
mleft(gx+hright)^2
Đọc tiếp
Gpt: \(x^4-3x^2-10x-4=0\)
Làm kiểu này được không ạ:
\(ax^4+bx^2+cx+d=0\\ \Leftrightarrow x^4+\dfrac{b}{a}x^2+\dfrac{c}{a}x+\dfrac{d}{a}=0\\ \Leftrightarrow\left(x^4+2yx^2+y^2\right)-2yx^2-y^2+\dfrac{b}{a}x^2+\dfrac{c}{a}x+\dfrac{d}{a}=0\\ \Leftrightarrow\left(x^2+2y\right)^2+x^2.\left(\dfrac{b}{a}-2y\right)+\dfrac{c}{a}x+\dfrac{d}{a}-y^2=0\)
Ta tìm y: \(x^2.\left(\dfrac{b}{a}-2y\right)+\dfrac{c}{a}x+\dfrac{d}{a}-y^2\\ =m\left(gx+h\right)^2\)
Giải các phương trình sau:
a \(x^4-x^2-56=0\)
b \(\left(x-2\right)^4+\left(x+2\right)^4=32\)
c \(\left(x+3\right)^4+\left(x+5\right)^4=16\)
d \(\left(6-x\right)^4+\left(8-x\right)^4=80\)
Cho 4 điểm A ( 0; -5) , B (-5 ;20 ) , C( 2 ; 1) , D( 2 ; 5 )
Cmr : 4 điểm A , B, C thẳng hàng
b. Tìm x sao cho 3 điểm A( x ; 14) , B( -5 ; 20 ) , C( 7 ; -16)