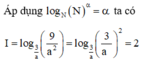Các câu hỏi tương tự
Cho a là số thực dương khác 2 .Tính
I
log
a
2
a
2
2
. A.
I
2
B.
I
-
1
2
C.
I
-
2
D.
I
1
2
Đọc tiếp
Cho a là số thực dương khác 2 .Tính I = log a 2 a 2 2 .
A. I = 2
B. I = - 1 2
C. I = - 2
D. I = 1 2
Cho a là số thực dương khác 1. Tính
I
log
a
a
. A.
I
1
2
B.
I
-
1
2
C. I -2 D. I 2
Đọc tiếp
Cho a là số thực dương khác 1. Tính I = log a a .
A. I = 1 2
B. I = - 1 2
C. I = -2
D. I = 2
Cho a là số thực dương khác 1. Tính I = log a a .
A. I = -2
B. I = 0
C. I = 1 2 .
D. I = 2
Cho a, b, c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau:(I)
2
a
3
⇔
a
log
2
3
(II)
∀
x
∈
ℝ
0
,
log
3
x
2
2
log
3
x
(III) ...
Đọc tiếp
Cho a, b, c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau:
(I) 2 a = 3 ⇔ a = log 2 3
(II) ∀ x ∈ ℝ \ 0 , log 3 x 2 = 2 log 3 x
(III) log a b . c = log a b . log a c
Trong ba mệnh đề (I), (II), (III), tổng số mệnh đề đúng là?
A. 3
B. 2
C. 1
D. 0
Cho a,b,c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau
I
3
a
2
⇔
a
log
3
2
I
I
∀
x
∈
ℝ
0
,
log
2
x
2...
Đọc tiếp
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
I 3 a = 2 ⇔ a = log 3 2 I I ∀ x ∈ ℝ \ 0 , log 2 x 2 = 2 log 2 x I I I log a b c = log a b . log a c
Trong ba mệnh đề I , I I , I I I số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho a là số thực dương khác 5. Tính
I
log
a
5
a
3
125
A.
I
-
1
3
B. I -3 C.
I
1
3
D. I 3
Đọc tiếp
Cho a là số thực dương khác 5. Tính I = log a 5 a 3 125
A. I = - 1 3
B. I = -3
C. I = 1 3
D. I = 3
Cho a, b, c là các số thực dương khác 1. Biết
log
a
c
2
,
log
b
c
3.
Tính
P
l
o
g
c
a
b
A.
P
5
6
B.
P
1
C.
P...
Đọc tiếp
Cho a, b, c là các số thực dương khác 1.
Biết log a c = 2 , log b c = 3. Tính P = l o g c a b
A. P = 5 6
B. P = 1
C. P = 2 3
D. P = 1 2
Cho số phức z thỏa mãn |z - 1 + 3i|+|z + 5 + i| 2
65
Giá trị nhỏ nhất của |z + 2 + i| đạt được khi z a + bi với a,b là các số thực dương. Giá trị của
2
a
2
+
b
2
bằng A. 17 B. 33 C. 24 D. 36
Đọc tiếp
Cho số phức z thỏa mãn
|z - 1 + 3i|+|z + 5 + i| = 2 65 Giá trị nhỏ nhất của
|z + 2 + i| đạt được khi z = a + bi với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
A. 17
B. 33
C. 24
D. 36
Cho A, B, C lần lượt là 3 điểm biểu diễn các số phức
z
1
−
4
i
1
−
i
;
z
2
(
1
+
i
)
(
1
+
2
i
)
;
z
3
2...
Đọc tiếp
Cho A, B, C lần lượt là 3 điểm biểu diễn các số phức z 1 = − 4 i 1 − i ; z 2 = ( 1 + i ) ( 1 + 2 i ) ; z 3 = 2 + 6 i 3 − i . Biết A, B, C tạo thành một tam giác, diện tích của tam giác đó là:
A. S=10
B. S=5
C. S = 5 2
D. S = 10 2