Các câu hỏi tương tự
Cho lăng trụ tam giác ABC.A’B’C’. Đặt
A
A
→
a
⇀
,
A
B
→
b
→
,
A
C
→
c
→
. Gọi I là điểm thuộc CC’ sao cho...
Đọc tiếp
Cho lăng trụ tam giác ABC.A’B’C’. Đặt A A ' → = a ⇀ , A B → = b → , A C → = c → . Gọi I là điểm thuộc CC’ sao cho C ' I → = 1 3 C ' C → , điểm G thỏa mãn G B → + G A ' → + G B ' → + G C ' → = 0 → . Biểu diễn véc tơ I G → qua véc tơ a → , b → , c → . Trong các khẳng định sau, khẳng định nào là khẳng định đúng
A. I G → = 1 4 1 3 a → + 2 b → - 3 c →
B. I G → = 1 3 1 3 a → + 2 b → - 3 c →
C. I G → = 1 4 a → + 2 b → - 3 c →
D. I G → = 1 4 - 1 3 a → + 2 b → - 3 c →
Cho hàm số
f
(
x
)
x
3
-
3
x
2
+
5
x
+
1
Hàm số yg(x) có bảng biến thiên như sauBiết rằng
a
,
b
∈
R
và ab;g(a).g(b)0 Phương trình g(f(x))0 có tất cả bao nhiêu nghiệm thực? A. 3 B. 9 C. 5 D. 1
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 3 x 2 + 5 x + 1 Hàm số y=g(x) có bảng biến thiên như sau
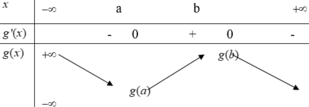
Biết rằng a , b ∈ R và a<b;g(a).g(b)<0 Phương trình g(f(x))=0 có tất cả bao nhiêu nghiệm thực?
A. 3
B. 9
C. 5
D. 1
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi thoả mãn
a
+
b
+
c
3
Khoảng cách từ gốc toạ độ O đến mặt phẳng (ABC) có giá trị lớn nhất bằng A.
3
B.
1
3
C.
3
3
D.
3...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi thoả mãn a + b + c = 3 Khoảng cách từ gốc toạ độ O đến mặt phẳng (ABC) có giá trị lớn nhất bằng
A. 3
B. 1 3
C. 3 3
D. 3 3
Cho hai số thực a, b với
a
0
,
a
≠
1
,
b
≠
0
. Khẳng định nào sau đây sai? A.
log
a
3
b
1
2
log
a
b
B.
1
2
log
a...
Đọc tiếp
Cho hai số thực a, b với a > 0 , a ≠ 1 , b ≠ 0 . Khẳng định nào sau đây sai?
A. log a 3 b = 1 2 log a b
B. 1 2 log a b 2 = log a b
C. 1 2 log a a 2 = 1
D. 1 2 log a b 2 = log a b
Cho các số thực dương a, b với a≠1 và log a b 0. Khẳng định nào sau đây là đúng? A.
0
a
,
b
1
0
a
1...
Đọc tiếp
Cho các số thực dương a, b với a≠1 và log a b >0. Khẳng định nào sau đây là đúng?
A. 0 < a , b < 1 0 < a < 1 < b
B. 0 < a , b < 1 1 < a , b
C. 0 < a , b < 1 0 < b < 1 < a
D. 0 < b < 1 < a 1 < a , b
Cho hai số thực a và b với
a
0
,
a
≠
1
,
b
≠
1
. Khẳng định nào sau đây là sai? A.
log
a
2
b
1
2
log
a
b...
Đọc tiếp
Cho hai số thực a và b với a > 0 , a ≠ 1 , b ≠ 1 . Khẳng định nào sau đây là sai?
A. log a 2 b = 1 2 log a b
B. 1 2 log a a 2 = 1
C. 1 2 log a b 2 = log a b
D. 1 2 log a b 2 = log a b
Cho đồ thị hàm số
y
−
x
3
+
3
m
x
+
1
có hai điểm cực trị A, B thỏa mãn tam giác OAB vuông tạo O (O là gốc tọa độ). Khẳng định nào dưới đây là đúng? A.
−
1
m
1
3
B.
1
m
3
C.
−...
Đọc tiếp
Cho đồ thị hàm số y = − x 3 + 3 m x + 1 có hai điểm cực trị A, B thỏa mãn tam giác OAB vuông tạo O (O là gốc tọa độ). Khẳng định nào dưới đây là đúng?
A. − 1 < m < 1 3
B. 1 < m < 3
C. − 1 2 < m < 1
D. − 2 < m < 0
Cho đồ thị hàm số
y
−
x
3
+
3
m
x
+
1
có hai điểm cực trị A, B thỏa mãn tam giác OAB vuông tạo O (O là gốc tọa độ). Khẳng định nào dưới đây là đúng? A.
−
1
m
1
3
B.
1
m
3
C.
−...
Đọc tiếp
Cho đồ thị hàm số y = − x 3 + 3 m x + 1 có hai điểm cực trị A, B thỏa mãn tam giác OAB vuông tạo O (O là gốc tọa độ). Khẳng định nào dưới đây là đúng?
A. − 1 < m < 1 3
B. 1 < m < 3
C. − 1 2 < m < 1
D. − 2 < m < 0
Cho hàm số
f
n
a
n
+
1
+
b
n
+
2
+
c
n
+
3
n
∈
ℕ
*
với a, b, c là hằng số thỏa mãn a + b + c 0. Khẳng định nào sau đây đúng? A.
l...
Đọc tiếp
Cho hàm số f n = a n + 1 + b n + 2 + c n + 3 n ∈ ℕ * với a, b, c là hằng số thỏa mãn a + b + c = 0. Khẳng định nào sau đây đúng?
A. l i m x → + ∞ f ( n ) = - 1
B. l i m x → + ∞ f ( n ) = 1
C. l i m x → + ∞ f ( n ) = 0
D. l i m x → + ∞ f ( n ) = 2




