\(C_RA=R\text{A}=\left(-\infty;-1\right)\cup[9;+\infty)\)
\(C^A_R=\left(-\infty;-1\right)\cup[9;+\infty)\)
Cho A = [−3;2). Tập hợp C R A là :
A. ( − ∞ ; − 3 )
B. ( 3 ; + ∞ ) . ( 3 ; + ∞ )
C. [ 2 ; + ∞ )
D. ( − ∞ ; − 3 ) ∪ [ 2 ; + ∞ )
Cho tập hợp C R A = [ − 3 ; 8 ) , C R B = ( − 5 ; 2 ) ∪ ( 3 ; 11 ) . Tập C R ( A ∩ B ) ) là:
A. ( − 3 ; 3 )
B. ∅
C. ( − 5 ; 11 )
D. ( − 3 ; 2 ) ∪ ( 3 ; 8 )
Cho các tập hợp: A = ( -∞; m) và B = [3m – 1; 3m +3]. Giá trị m để CRA ∩ B ≠ ∅ là:
A. m < -3/2
B. m ≤ -3/2
C. m > -3/2
D. m ≥ -3/2
Cho các tập hợp khác rỗng A = (− ∞ ; m) và B = [2m−2; 2m+2]. Tìm m ∈ R để ( C R A ) ∩ B ≠ ∅ .
A. m ≥ 2
B. m < - 2
C. m ≥ − 2
D. m < 2
Cho C R A = ( − ∞ ; 3 ) ∪ [ 5 ; + ∞ ) v à C R B = [ 4 ; 7 ) . Xác định tập X = A ∩ B.
A. X = [5;7)
B. X = (5;7)
C. X = (3;4)
D. X = [3;4).
cho tam giác ABC có a(1;5);b(-5;2);c(-1;9). tìm M trên đường thẳng BC sao cho AM có độ dài ngắn nhất
Cho A và B là hai tập hợp con của tập hợp E được biểu diễn bởi biểu đồ Ven dưới đây
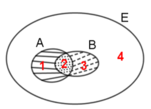
Trong các phát biểu sau
I. Vùng 1 là tập hợp A \ B.
II. Vùng 2 là tập hợp A ∩ B.
III. Vùng 3 là tập hợp B \ A.
IV. Vùng 4 là tập hợp E \ (A ∪ B).
Số phát biểu đúng là:
A. 1.
B. 2.
C. 3.
D. 4.
cho tập hợp A có 5 phần tử.Hỏi tập hợp A có bao nhiêu tập hợp con không phải là tập hợp rỗng?
Cho tập hợp A = {a; b; c; d; e; f}. Số tập hợp con của tập hợp A là:
A. 6
B. 12
C. 64
D. 32
Cho A là tập hợp các ước nguyên dương của 9 B là tập hợp các ước nguyên dương của 12.khi đó tập hợp A giao B
