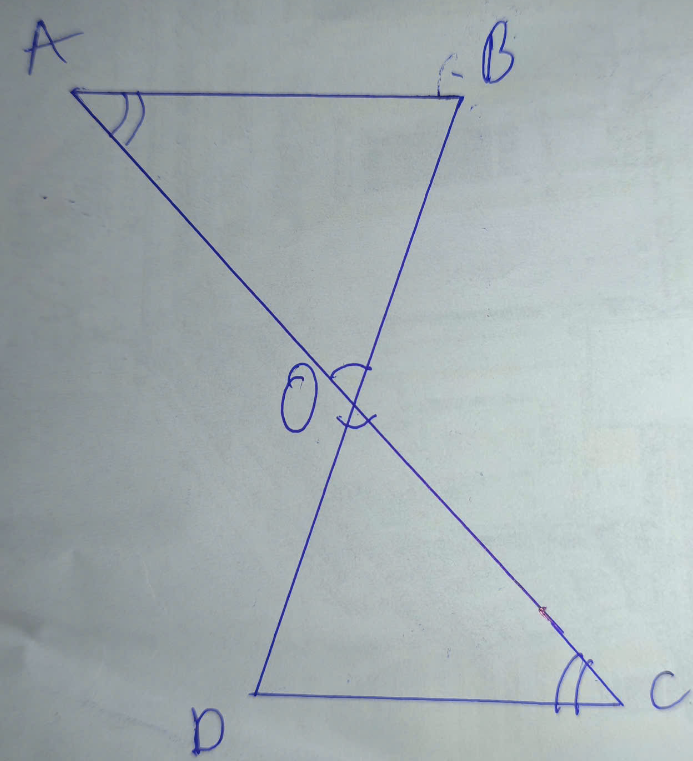
xét tam giác OAB và tam giác OCD có:
góc AOB = góc COD (đối đỉnh)
góc OAB = góc OCD (so le trong)
=> tam giác OAB đồng dạng tam giác OCD (g-g)
\(=>\dfrac{AB}{CD}=\dfrac{OA}{OC}\\ =>AB\cdot OC=OA\cdot CD\)
Cho tứ giác ABCD có các cạnh và các đường chéo thoả mãn điều kiện: \(AB+BD\le AC+CD\)
Chứng minh AB<AC
Cho hình thang ABCD (AB // CD, AB < CD).Hai đường chéo AC và BD cắt nhau tại O. Qua A vẽ đường thẳng song song với BC cắt BD ở E và cắt CD ở K. Qua B kẻ đường thẳng song song với AD cắt AC ở F và cắt CD ở I. Chứng minh rằng:
a) EF // CD
b) AB2 = CD.EF
Cho tứ giác ABCD. Các đường chéo AC và BD cắt nhau tại O. Các cạnh AD và BC kéo dài cắt nhau tại E. Biết AC _|_ AD, DB _|_ BC.
a) Chứng minh rằng đường thẳng d qua các trung điểm OE và CD là trục đối xứng của cạnh AB.
b) Tứ giác ABCD phải có điều kiện gì để d và OE trùng nhau?
Bài 1: Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N.
1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
Cho hình thang ABCD có AB // CD. Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với BC, cắt AB tại E. Đường thẳng qua O song song với CD cắt AD tại F
1) Chứng minh rằng: OA.CD = OC.AB
2) Chứng minh rằng: EF // BD
3) Biết: AE = 3cm, EB = 5cm, BD = 12cm. Tính độ dài cạnh EF?
em cảm ơn
Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N. 1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
Cho hình thang ABCD (CD > AB) với AB // CD và AB ┴ BD. Hai đường chéo AC và BD cắt nhau tại G. Trên đường thẳng vuông góc với AC tại C lấy điểm E sao cho CE = AG và đoạn thẳng GE khong cắt đường thẳng CD. Trên đoạn thẳng CD lấy điểm F sao cho DF = GB. Chứng minh GF ┴ EF
cho hình thang ABCD(AB song song với CD) có hai đường chéo AC và BD cắt nhau tại O. Qua O kẻ đường thẳng song song với hai đáy cắt AD và BC lần lượt tại P và Q. Biết AB=a; CD=b, cmr độ dài PQ là trung bình điều hòa của AB và CD
Cho tứ giác lồi ABCD có hai đường chéo AC và BD vuông góc với nhau và cắt nhau
tại O. Biết rằng BAC=BDC . Từ O kẻ đường thẳng vuông góc với CD cắt AB tại I .
Chứng minh I là trung điểm AB
Cho hình thang ABCD có AB//CD (AB<CD), M là trung điểm AD. Qua M vẽ đường thẳng // với 2 đáy của hình thang cắt 2 đường chéo BD và AC lần lượt tại E,F.
a) Chứng minh N, E, F lần lượt là trung điểm của BC, BD, AC
b) Gọi I là trưng điểm AB, đường thẳng vuông góc với IE cắt với nhau tại E và đường thẳng vuông góc với IF tại F cắt nhau tại K. Chứng minh KC=KD
