Các câu hỏi tương tự
Cho hàm số y f(x) xác định trên khoảng (0; +∞) và thỏa mãn
lim
x
→
+
∞
f
(
x
)
1
Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau: A. Đường thẳng y 1 là tiệm cận ngang của đồ thị hàm số y f(x) B. Đường thẳng x 1 là tiệm cận đứng của đồ thị hàm số y f(x) C. Đường thẳng x 1 là tiệm cận n...
Đọc tiếp
Cho hàm số y = f(x) xác định trên khoảng (0; +∞) và thỏa mãn lim x → + ∞ f ( x ) = 1 Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau:
A. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số y = f(x)
B. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số y = f(x)
C. Đường thẳng x = 1 là tiệm cận ngang của đồ thị hàm số y = f(x)
D. Đường thẳng y = 1 là tiệm cận đứng của đồ thị hàm số y = f(x)
Gọi F(x) là nguyên hàm trên R của hàm số
f
(
x
)
x
2
e
a
x
(
a
≠
0
)
sao cho
F
1
a
F
(
0
)
+
1
. Chọn mệnh đề đúng trong các mệnh đề sau.
Đọc tiếp
Gọi F(x) là nguyên hàm trên R của hàm số f ( x ) = x 2 e a x ( a ≠ 0 ) sao cho F 1 a = F ( 0 ) + 1 . Chọn mệnh đề đúng trong các mệnh đề sau.
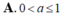
![]()
![]()
![]()
Gọi F(x) là nguyên hàm trên R của hàm số
f
x
x
2
e
ax
(
a
≠
0
)
, sao cho
F
1
a
F
(
0
)...
Đọc tiếp
Gọi F(x) là nguyên hàm trên R của hàm số f x = x 2 e ax ( a ≠ 0 ) , sao cho F 1 a = F ( 0 ) + 1 . Chọn mệnh đề đúng trong các mệnh đề sau.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho a; b 0 và
a
,
b
≠
1
, x và y là hai số thực dương. Tìm mệnh đề đúng trong các mệnh đề sau:
Đọc tiếp
Cho a; b > 0 và a , b ≠ 1 , x và y là hai số thực dương. Tìm mệnh đề đúng trong các mệnh đề sau:
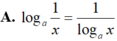
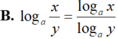
![]()
![]()
Cho hàm số y f(x) xác định trên các khoảng (0; +∞) và thỏa mãn
lim
x
→
∞
f
(
x
)
2
. Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau? A. Đường thẳng y 2 là tiệm cận đứng của đồ thị hàm số y f(x). B. Đường thẳng x 2 là tiệm cận ngang của đồ thị hàm số y f(x) C. Đường thẳng y 2 là tiệm cận ngang của đồ thị...
Đọc tiếp
Cho hàm số y = f(x) xác định trên các khoảng (0; +∞) và thỏa mãn lim x → ∞ f ( x ) = 2 . Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau?
A. Đường thẳng y = 2 là tiệm cận đứng của đồ thị hàm số y = f(x).
B. Đường thẳng x = 2 là tiệm cận ngang của đồ thị hàm số y = f(x)
C. Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số y = f(x)
D. Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số y = f(x)
Cho
0
a
≠
1
và
b
∈
ℝ
. Chọn mệnh đề sai trong các mệnh đề sau
Đọc tiếp
Cho 0 < a ≠ 1 và b ∈ ℝ . Chọn mệnh đề sai trong các mệnh đề sau
![]()
![]()
![]()
![]()
Cho a; b 0 thỏa mãn a2 + b 2 7ab. Chọn mệnh đề đúng trong các mệnh đề sau? A. 3log(a+b)
1
2
(loga+logb) B.
log
a
+
b
3
1
2
(
log
a
+
log
b
)
C. 2( loga + logb) log( 7ab) . D. log(a+b)...
Đọc tiếp
Cho a; b > 0 thỏa mãn a2 + b 2 = 7ab. Chọn mệnh đề đúng trong các mệnh đề sau?
A. 3log(a+b) = 1 2 (loga+logb)
B. log a + b 3 = 1 2 ( log a + log b )
C. 2( loga + logb) = log( 7ab) .
D. log(a+b) = 3 2 (loga+logb)
Cho a 0 và
a
≠
1
. Tìm mệnh đề đúng trong các mệnh đề sau:
A
.
log
a
(
x
,
y
)
log
a
x
.
log
a
y
;
∀
x
,
y
∈
ℝ
B
....
Đọc tiếp
Cho a > 0 và a ≠ 1 . Tìm mệnh đề đúng trong các mệnh đề sau:
A . log a ( x , y ) = log a x . log a y ; ∀ x , y ∈ ℝ
B . log a x n = n log a x ( ∀ x > 0 , n ≠ 0 )
C . log a x c ó n g h ĩ a ∀ x ∈ ℝ
D . log a 1 = a
Cho a 0 và a khác 1 . Tìm mệnh đề đúng trong các mệnh đề sau A.
log
a
(
x
y
)
l
og
a
x
.
log
a
y
(
∀
x
,
y
∈
R
)
B.
log
a...
Đọc tiếp
Cho a > 0 và a khác 1 . Tìm mệnh đề đúng trong các mệnh đề sau
A. log a ( x y ) = l og a x . log a y ( ∀ x , y ∈ R )
B. log a x n = n log a x ( ∀ n > 0 . n ≠ 0 )
C. log a x c ó n g h ĩ a ∀ x ∈ R
D. log a 1 = a



