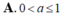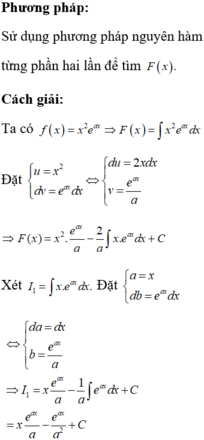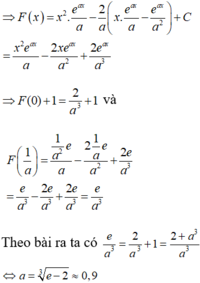Các câu hỏi tương tự
Gọi F(x) là nguyên hàm trên R của hàm số
f
x
x
2
e
ax
(
a
≠
0
)
, sao cho
F
1
a
F
(
0
)...
Đọc tiếp
Gọi F(x) là nguyên hàm trên R của hàm số f x = x 2 e ax ( a ≠ 0 ) , sao cho F 1 a = F ( 0 ) + 1 . Chọn mệnh đề đúng trong các mệnh đề sau.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số F(x) là một nguyên hàm của hàm số
f
(
x
)
2
cos
x
-
1
sin
2
x
trên khoảng
0
;
π
. Biết rằng giá trị lớn nhất của F(x) trên khoảng
0...
Đọc tiếp
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?

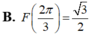
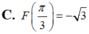
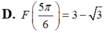
Cho hàm số
y
f
x
xác định, có đạo hàm trên đoạn
a
;
b
(với
a
b
). Xét các mệnh đề sau: i) Nếu
f
x...
Đọc tiếp
Cho hàm số y = f x xác định, có đạo hàm trên đoạn a ; b (với a < b ). Xét các mệnh đề sau:
i) Nếu f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên khoảng a ; b .
ii) Nếu phương trình f ' ( x ) = 0 có nghiệm x 0 thì f ' ( x ) đổi dấu từ dương sang âm khi qua x 0 .
iii) Nếu f ' x ≤ 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
Số mệnh đề đúng trong các mệnh đề trên là:
A. 2
B. 3
C. 0
D. 1
Cho hàm số y f(x) xác định trên khoảng (0; +∞) và thỏa mãn
lim
x
→
+
∞
f
(
x
)
1
Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau: A. Đường thẳng y 1 là tiệm cận ngang của đồ thị hàm số y f(x) B. Đường thẳng x 1 là tiệm cận đứng của đồ thị hàm số y f(x) C. Đường thẳng x 1 là tiệm cận n...
Đọc tiếp
Cho hàm số y = f(x) xác định trên khoảng (0; +∞) và thỏa mãn lim x → + ∞ f ( x ) = 1 Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau:
A. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số y = f(x)
B. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số y = f(x)
C. Đường thẳng x = 1 là tiệm cận ngang của đồ thị hàm số y = f(x)
D. Đường thẳng y = 1 là tiệm cận đứng của đồ thị hàm số y = f(x)
Cho hàm số y f(x) xác định trên các khoảng (0; +∞) và thỏa mãn
lim
x
→
∞
f
(
x
)
2
. Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau? A. Đường thẳng y 2 là tiệm cận đứng của đồ thị hàm số y f(x). B. Đường thẳng x 2 là tiệm cận ngang của đồ thị hàm số y f(x) C. Đường thẳng y 2 là tiệm cận ngang của đồ thị...
Đọc tiếp
Cho hàm số y = f(x) xác định trên các khoảng (0; +∞) và thỏa mãn lim x → ∞ f ( x ) = 2 . Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau?
A. Đường thẳng y = 2 là tiệm cận đứng của đồ thị hàm số y = f(x).
B. Đường thẳng x = 2 là tiệm cận ngang của đồ thị hàm số y = f(x)
C. Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số y = f(x)
D. Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số y = f(x)
Câu 22. Cho hàm số yf(x)��(�) có đạo hàm trên khoảng (a;b)(�;�). Tìm mệnh đề sai trong các mệnh đề sau.A. Nếu hàm số yf(x)��(�) đồng biến trên (a;b)(�;�) thì f′(x)0�′(�)0 với mọi x∈(a;b)�∈(�;�).B. Nếu hàm số yf(x)��(�) nghịch biến trên (a;b)(�;�) thì f′(x)≤0�′(�)≤0 với mọi x∈(a;b)�∈(�;�).C. Nếu f′(x)0�′(�)0 với mọi x∈(a;b)�∈(�;�) thì hàm số yf(x)��(�) đồng biến trên (a;b)(�;�).D. Nêu f′(x)0�′(�)0 với mọi x∈(a;b)�∈(�;�) thì hàm số yf(x)��(�) nghịch biến trên (a;b)(�;�).
Đọc tiếp
Câu 22. Cho hàm số có đạo hàm trên khoảng . Tìm mệnh đề sai trong các mệnh đề sau.A. Nếu hàm số đồng biến trên thì với mọi .B. Nếu hàm số nghịch biến trên thì với mọi .C. Nếu với mọi thì hàm số đồng biến trên .D. Nêu với mọi thì hàm số nghịch biến trên .
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị hàm số yf (x) như hình vẽ bên dưới. Xét hàm số g(x)f(x^2-3) và các mệnh đề sau: I. Hàm số có 3 điểm cực trị. II. Hàm số g(x)đạt cực tiểu tại x0 III. Hàm số g(x) đạt cực đại tại x2 IV. Hàm số g(x) đồng biến trên khoảng (-2;0) V. Hàm số g(x) nghịch biến trên khoảng (-1;1) Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A.1 B.4 C.3 D.2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số ![]() có 3 điểm cực trị.
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
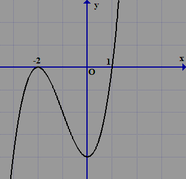
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2
Cho hàm số y f(x) liên tục trên R. Biết đồ thị hàm số y f’(x) được cho bởi hình vẽ bên, xét hàm số
y
g
x
f
x
-
x
2
2
. Hỏi trong các mệnh đề sau có bao nhiêu mệnh đề đúng? (I) Số điểm cực tiểu của hàm số g(x) là 2. (II) Hàm số g(x) đồng biến trên khoảng (-1;2). (III) Giá trị nhỏ nhất của hàm số là g(-1). (IV) Cực đại của hàm số g(x)...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R. Biết đồ thị hàm số y = f’(x) được cho bởi hình vẽ bên, xét hàm số y = g x = f x - x 2 2 . Hỏi trong các mệnh đề sau có bao nhiêu mệnh đề đúng?

(I) Số điểm cực tiểu của hàm số g(x) là 2.
(II) Hàm số g(x) đồng biến trên khoảng (-1;2).
(III) Giá trị nhỏ nhất của hàm số là g(-1).
(IV) Cực đại của hàm số g(x) là 0.
A. 0
B. 1
C. 2
D. 3
Cho F(x) là một nguyên hàm của hàm số
f
(
x
)
1
x
-
1
thỏa mãn F(5) 2 và F(0) 1. Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 x - 1 thỏa mãn F(5) = 2 và F(0) = 1. Mệnh đề nào dưới đây đúng?
![]()
![]()
![]()
![]()