a) \(A=\left(\dfrac{1}{2x-y}+\dfrac{3y-x^2-2}{y^2-4x^2}-\dfrac{2}{2x+y}\right):\left(\dfrac{x^2+y^2}{4x^2-y^2}+1\right)\)
\(A=\left[\dfrac{2x+y}{\left(2x-y\right)\left(2x+y\right)}+\dfrac{x^2+2-3y}{\left(2x-y\right)\left(2x+y\right)}-\dfrac{2\left(2x-y\right)}{\left(2x+y\right)\left(2x-y\right)}\right]:\dfrac{x^2+y^2+4x^2-y^2}{4x^2-y^2}\)
\(A=\dfrac{2x+y+x^2+2-3y-4x+2y}{\left(2x+y\right)\left(2x-y\right)}.\dfrac{\left(2x-y\right)\left(2x+y\right)}{6x^2}\)
\(A=\dfrac{x^2-2x+2}{5x^2}\)
b) \(\left|x-1\right|=2\Leftrightarrow\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\left(l\right)\end{matrix}\right.\)
Có x,y bạn tự thay vô bấm máy ra nha.
c) Ta có: \(x^2-2x\ge0\forall x\), \(5x^2\ge0\forall x\)
\(\Rightarrow A>0\)
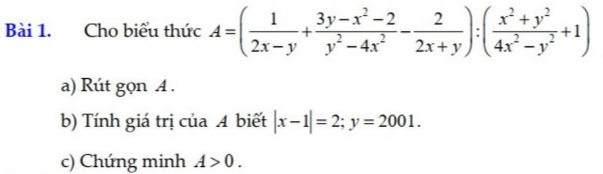
không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
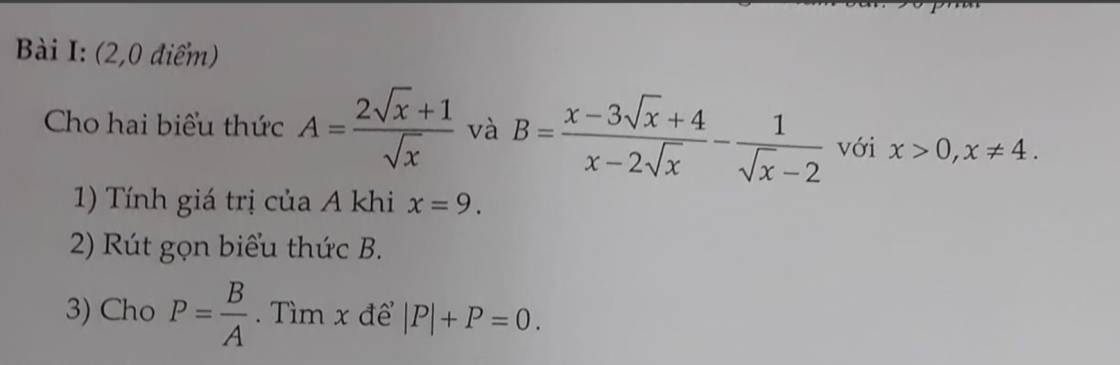
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
