\(2a=12\Rightarrow a=6\)
\(2c=8\sqrt{2}\Rightarrow c=4\sqrt{2}\)
\(\Rightarrow b^2=a^2-c^2=4\)
Phương trình: \(\dfrac{x^2}{36}+\dfrac{y^2}{4}=1\)
Cho elip (E) có phương trình x 2 m 2 + y 2 6 m = 1 . Giá trị của m để phương trình đó là phương trình chính tắc của một elip có tiêu cự bằng 8 là:
A. m = - 2
B. m = 8
C. m = - 2 hoặc m = 8
D. không tồn tại m
Elip x2/16+y2/9=1 có hai tiêu điểm F1, F2; M là một điểm bất kì nằm trên elip. Tính MF1+MF2 A.10. B.8 C.6 D.12
Phương trình chính tắc của elip có độ dài trục nhỏ bằng 12, độ dài tiêu cự bằng 8 là
A. x 2 36 + y 2 20 = 1
B. x 2 52 + y 2 36 = 1
C. x 2 208 + y 2 144 = 1
D. x 2 144 + y 2 80 = 1
Phương trình chính tắc của elip có độ dài trục lớn bằng 8, độ dài tiêu cự bằng 6 là:
A. x 2 64 + y 2 36 = 1
B. 16 x 2 + 7 y 2 = 112
C. 7 x 2 + 16 y 2 = 112
D. x 2 16 + y 2 7 = 1
Phương trình chính tắc của elip có độ dài trục lớn bằng 8, độ dài tiêu cự bằng 6 là:
A. x 2 64 + y 2 28 = 1
B. 16 x 2 + 7 y 2 = 112
C. 7 x 2 + 16 y 2 = 1
D. x 2 16 + y 2 7 = 1
Phương trình chính tắc của elip có độ dài trục bé và tiêu cự đều bằng 6 là:
A. x 2 9 + y 2 18 = 1
B. x 2 18 + y 2 9 = 1
C. x 2 9 + y 2 9 = 1
D. 9 x 2 + 18 y 2 = 1
Cho elip có phương trình: x 2 16 + y 2 4 = 1 . Gọi M là điểm thuộc E sao cho MF1= MF2. Khi đó tọa độ điểm M1; M2 là:
A.M1(0 ; 1) và M2(0; -1).
B. M1(0 ; 2) và M2(0; -2).
C. M1(0 ; 3) và M2(0; -3).
D. M1(0 ; 4) và M2(0; -4).
Phương trình chính tắc của elip có độ dài trục lớn bằng hai lần độ dài trục nhỏ và tiêu cự bằng 6 là:
A. x 2 64 + y 2 36 = 1
B. x 2 12 + y 2 3 = 1
C. x 2 9 + y 2 12 = 1
D. 9 x 2 + 12 y 2 = 108
Tìm phương trình chính tắc của hyperbol nếu nó có tiêu cự bằng 12 và độ dài trục thực bằng 10.
A.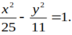 
B.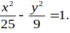 
C.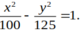 
D.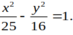 
Cho phương trình x 2 4 m + 1 + y 2 3 m = 1 . Để phương trình đã cho là phương trình chính tắc của một elip có tiêu cự bằng 8 thì:
A. m = 7
B. m = 63
C. m = 15
D. m = 1
