Đáp án B
+Phương trình chính tắc của elip có dạng:
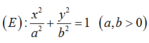
Nên a= 4; b= 2
+Vì MF1= MF2 nên M thuộc đường trung trực của F1F2 chính là trục Oy
+ M là điểm thuộc (E) nên M là giao điểm của elip và trục Oy
Vậy . M1(0 ; 2) và M2(0; -2).
Đáp án B
+Phương trình chính tắc của elip có dạng:
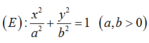
Nên a= 4; b= 2
+Vì MF1= MF2 nên M thuộc đường trung trực của F1F2 chính là trục Oy
+ M là điểm thuộc (E) nên M là giao điểm của elip và trục Oy
Vậy . M1(0 ; 2) và M2(0; -2).
Cho đường tròn (C) (x-1)2 + (y-1)2 = 25
(Cm) (x-2)2 + (y-m)2 = 16
Gọi m1, m2 là các giá trị thỏa mãn khoảng cách giữa hai giao điểm của C và Cm là lớn nhất Khẳng định nào sau đấy đúng
A. 1« m1 + m2 < 4
B. -1 « m1 + m2 <1
C. m1 + m2 » 4
D. m1 + m2 <-1
Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung AM = α (0 < α < π/2). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc tọa độ. Tìm số đo các cung AM1, AM2, AM3.
Phương trình của elip có 1 tiêu điểm F 2 ( 1 ; 0 ) và đi qua điểm M 2 ; - 2 5 là:
A. x 2 9 + y 2 8 = 1
B. 4 x 2 + 5 y 2 = 1
C. x 2 5 + y 2 4 = 1
D. 5 x 2 + 4 y 2 = 1
Cho các phương trình có tham số m sau:
m x + m = 0 (1); m - 2 x + 2 m = 0 (2);
m 2 + 1 x + 2 = 0 (3) ; m 2 x + 3 m + 2 = 0 (4).
Phương trình luôn có nghiệm duy nhất với mọi giá trị của m là:
A. Phương trình (1)
B. Phương trình (2)
C. Phương trình (3)
D. Phương trình (4)
Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là F 1 - 3 ; 0 và điểm M 1 ; 3 2 nằm trên elip.
phương trình mx2 + 2( 2m - 3 )x+m2-4=0 có 2 nghiệm trái dấu khi và chỉ khi
Cho elip có phương trình:x2/16+y2/4=1.M là điểm thuộc (E) sao cho MF1=MF2.Khi đó tọa độ điểm M là?
Bài 3: Một phân xưởng có hai máy đặc chủng M1, M2 sản xuất hai loại sản phẩm kí hiệu là I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại I phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại II phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ trong một ngày, máy M2 một ngày chỉ làm việc không quá 4 giờ. Hãy đặt kế hoạch sản xuất sao cho tổng số tiền lãi cao nhất.
Cho elip 3x2 + 4y2 – 48 = 0 và đường thẳng d: x - 2y + 4 = 0. Giao điểm của d và Elip là
A. (0; - 4); (-2; -3) B. (4; 0); (3; 2) C. (0; 4); (-2; 3) D. (-4; 0); (2; 3)