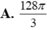Câu 44: Trong không gian Oxyz, cho mặt cầu \(\left(S\right)=\left(x-1\right)^2+\left(y+2\right)^2+\left(z-3\right)^2=48\). Gọi \(\left(\alpha\right)\) là mặt phẳng đi qua hai điểm \(A\left(0;0;-4\right)\) , \(B\left(2;0;0\right)\) và cắt mặt cầu \(\left(S\right)\) theo giao tuyến là đường tròn \(\left(C\right)\). Khối nón \(\left(N\right)\) có đỉnh là tâm của \(\left(S\right)\), đường tròn đáy là \(\left(C\right)\) có thể tích lớn nhất bằng:
A. \(\dfrac{128\pi}{3}\) B. \(39\pi\) C. \(\dfrac{88\pi}{3}\) D. \(\dfrac{215\pi}{3}\)
Mặt cầu (S) tâm \(I\left(1;-2;3\right)\) bán kính \(R=4\sqrt{3}\)
Giả sử (P) (ghi là (P) thay vì alpha cho dễ gõ kí tự) cắt trục Oy tại \(C\left(0;c;0\right)\), phương trình (P) có dạng:
\(\dfrac{x}{2}+\dfrac{y}{c}+\dfrac{z}{-4}=1\) \(\Leftrightarrow2c.x+4y-c.z-4c=0\)
Chiều cao nón: \(h=d\left(I;\left(P\right)\right)=\dfrac{\left|2c-8-3c-4c\right|}{\sqrt{4c^2+16+c^2}}=\dfrac{\left|5c+8\right|}{\sqrt{5c^2+16}}\)
\(\Rightarrow h^2=\dfrac{\left(5c+8\right)^2}{5c^2+16}=9-\dfrac{20\left(c-2\right)^2}{5c^2+19}\le9\)
\(\Rightarrow0\le h\le3\)
Bán kính đáy nón: \(r=\sqrt{R^2-h^2}=\sqrt{48-h^2}\)
\(V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi.\left(48-h^2\right).h=\dfrac{1}{3}\pi\left(48h-h^3\right)\)
Xét hàm \(f\left(h\right)=48h-h^3\) trên \(\left[0;3\right]\)
\(f'\left(h\right)=48-3h^2>0;\forall h\in\left[0;3\right]\)
\(\Rightarrow f\left(h\right)\) đồng biến \(\Rightarrow V_{max}=V\left(3\right)=\dfrac{1}{3}\pi.\left(48.3-3^3\right)=39\pi\)