Đặt \(AB=2a;BC=a\)
Tọa độ \(A\left(0;0\right);B\left(2a;0\right);C\left(2a;a\right);D\left(0;a\right);N\left(x;a\right)\)
\(\overrightarrow{AC}=2a;a\Rightarrow\overrightarrow{n_p}=\left(-a;2a\right)=-a\left(1;-2\right)\)
\(\Rightarrow\left(AC\right):\left(x-0\right)-2\left(y-0\right)=0\)
\(\Rightarrow\left(AC\right):y=\dfrac{1}{2}x\)
Hệ số góc của phương trình đường thẳng \(BN\) là \(\dfrac{a-0}{x-2a}=\dfrac{a}{x-2a}\)
Ta có \(AC\perp BN\)
\(\Leftrightarrow\dfrac{a}{x-2a}.\dfrac{1}{2}=-1\)
\(\Leftrightarrow\dfrac{a}{2\left(x-2a\right)}=-1\)
\(\Leftrightarrow a=-2\left(x-2a\right)\)
\(\Leftrightarrow x=\dfrac{3a}{2}\)
\(\Rightarrow N\left(\dfrac{3a}{2};a\right)\)
\(DN=\sqrt{\left(\dfrac{3a}{2}-0\right)^2-\left(a-a\right)^2}=\dfrac{3a}{2}\)
\(CN=\sqrt{\left(\dfrac{3a}{2}-2a\right)^2+\left(a-a\right)^2}=\dfrac{a}{2}\)
\(\Rightarrow\dfrac{DN}{CN}=\dfrac{\dfrac{3a}{2}}{\dfrac{a}{2}}=3\)


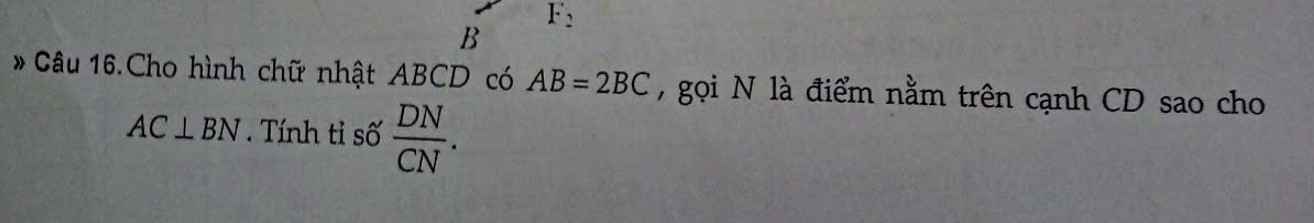













 e đg cần gấp ạ
e đg cần gấp ạ


