Bài 2:
1:
a: \(=x\left(x+2y\right)+2\left(x+2y\right)=\left(x+2y\right)\left(x+2\right)\)
b: \(=\left(3x-1\right)\left(3x+1\right)+2y\left(3x+1\right)=\left(3x+1\right)\left(3x-1+2y\right)\)
2:
a: \(\Leftrightarrow\left(x-5\right)\left(x+1\right)=0\)
=>x=5 hoặc x=-1
b: \(\Leftrightarrow\left(x+1\right)^2-\left(x+3\right)\left(x-3\right)=2x+10\)
\(\Leftrightarrow x^2+2x+1-x^2+9=2x+10\)
=>2x+10=2x+10(luôn đúng)
Vậy: S=R\{-1;3}
Bài 5:
Đặt \(\left\{{}\begin{matrix}a+b-c=x>0\\b+c-a=y>0\\c+a-b=z>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2b=x+y\\2c=y+z\\2a=z+x\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=\dfrac{x+y}{2}\\c=\dfrac{y+z}{2}\\a=\dfrac{z+x}{2}\end{matrix}\right.\)
\(\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)=xyz=\sqrt{xy}.\sqrt{yz}.\sqrt{zx}\le\dfrac{x+y}{2}.\dfrac{y+z}{2}.\dfrac{z+x}{2}=abc\left(đpcm\right)\)















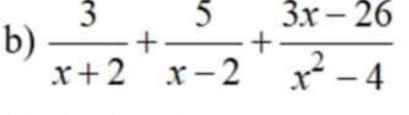 Cho mình xin lời giải chi tiết luôn ạ cực gấp xin cảm ơn ạ
Cho mình xin lời giải chi tiết luôn ạ cực gấp xin cảm ơn ạ


 nhanh mọi người ơi đang cần rất rất gấp luôn á
nhanh mọi người ơi đang cần rất rất gấp luôn á 



