Bài 3:
1: \(2^x=8^3\)
=>\(2^x=\left(2^3\right)^3=2^9\)
=>x=9
2: \(2^x=8^9\)
=>\(2^x=\left(2^3\right)^9=2^{27}\)
=>x=27
3: \(\left(\dfrac{1}{5}\right)^x=\left(\dfrac{1}{125}\right)^5\)
=>\(\left(\dfrac{1}{5}\right)^x=\left(\dfrac{1}{5}\right)^{5\cdot3}=\left(\dfrac{1}{5}\right)^{15}\)
=>x=15
4: \(2^{7x+4}=32^{12}\)
=>\(2^{7x+4}=\left(2^5\right)^{12}=2^{60}\)
=>7x+4=60
=>7x=56
=>x=8
5: \(3^{3-2x}=27^{13}\)
=>\(3^{-2x+3}=3^{3\cdot13}=3^{39}\)
=>-2x+3=39
=>-2x=36
=>x=-18
6: \(3^{6-3x}=81^3\)
=>\(3^{-3x+6}=3^{12}\)
=>-3x+6=12
=>-3x=6
=>x=-2
7: \(4^{-5x-1}=16^{12}\)
=>\(4^{-5x-1}=4^{24}\)
=>-5x-1=24
=>-5x=25
=>x=-5
8: \(5^{2x+1}=125^{x+25}\)
=>\(5^{2x+1}=5^{3\cdot\left(x+25\right)}\)
=>3(x+25)=2x+1
=>3x+75=2x+1
=>x=-74
l, \(2\left(\dfrac{3}{2}-x\right)-\dfrac{1}{3}=7x-\dfrac{1}{4}\)
\(2.\dfrac{3}{2}-2x-\dfrac{1}{3}=7x-\dfrac{1}{4}\)
\(3-2x-\dfrac{1}{3}=7x-\dfrac{1}{4}\)
\(-2x-7x=-\dfrac{1}{4}-3+\dfrac{1}{3}\)
\(x\left[\left(-2\right)-7\right]=\dfrac{-3}{12}-\dfrac{36}{12}+\dfrac{4}{12}\)
\(-9x=\dfrac{-35}{12}\)
\(x=\dfrac{-35}{12}:\left(-9\right)\)
\(x=\dfrac{-35}{12}.\dfrac{-1}{9}\)
\(x=\dfrac{35}{108}\)
Vậy \(x=\dfrac{35}{108}\)
\(4x-\left(2x+1\right)=3-\dfrac{1}{3}+x\)
\(4x-2x-1=\dfrac{9}{3}-\dfrac{1}{3}+x\)
\(x\left(4-2\right)-1=\dfrac{8}{3}+x\)
\(x.2-x=\dfrac{8}{3}+1\)
\(x\left(2-1\right)=\dfrac{8}{3}+\dfrac{3}{3}\)
\(x=\dfrac{11}{3}\)
Vậy \(x=\dfrac{11}{3}\)










 mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17
mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17
 các bạn giải giúp m với ạ! Mình đang cần gấp bài 2 và bài 3II
các bạn giải giúp m với ạ! Mình đang cần gấp bài 2 và bài 3II

 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
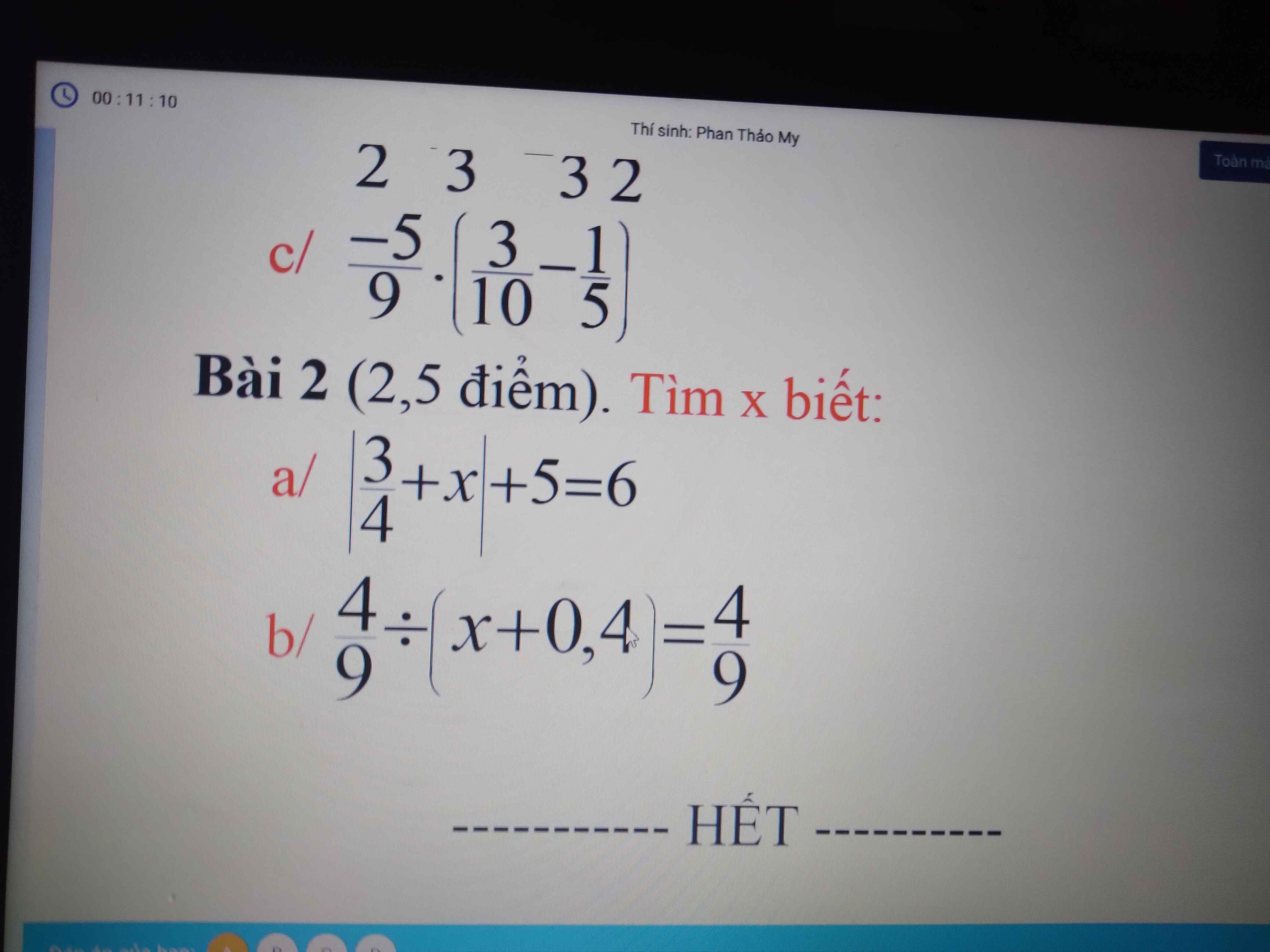





 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ


