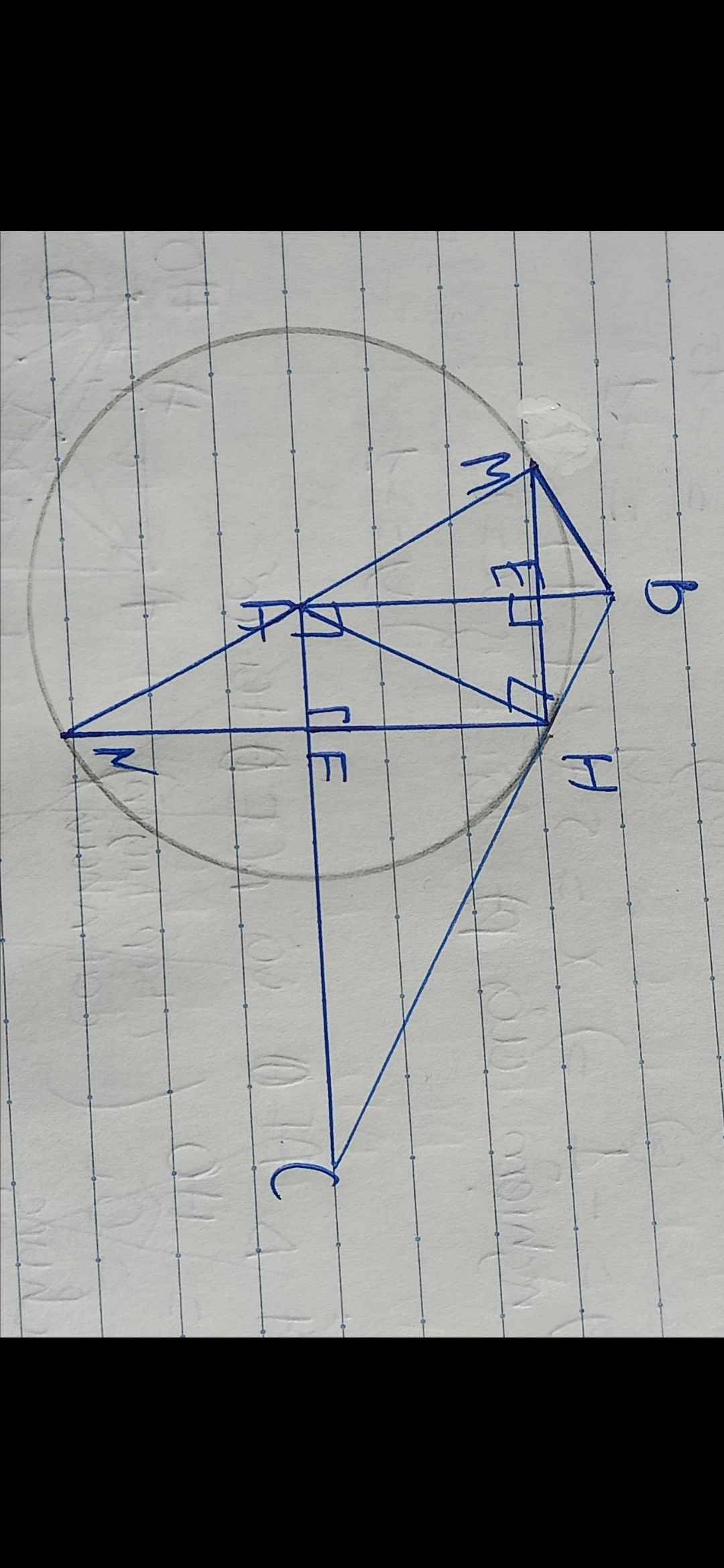
a: ΔAHC vuông tại H
=>AH<AC
=>R<AC
=>C nằm ngoài (A)
b: Xét (A) có
AH là bán kính
BC\(\perp\)AH tại H
Do đó: BC là tiếp tuyến của (A)
=>BC tiếp xúc với (A) tại H
c: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
d: ΔAHM cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAM
Xét ΔAHB và ΔAMB có
AH=AM
\(\widehat{HAB}=\widehat{MAB}\)
AB chung
Do đó: ΔAHB=ΔAMB
=>\(\widehat{AHB}=\widehat{AMB}=90^0\)
=>BM là tiếp tuyến của (A;AH)
e: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
nên AEHF là hình chữ nhật
=>\(\widehat{FHE}=90^0\)
=>\(\widehat{MHN}=90^0\)
=>ΔHMN vuông tại H
=>ΔHMN nội tiếp đường tròn đường kính MN
mà ΔHMN nội tiếp (A)
nên A là trung điểm của MN
=>M,A,N thẳng hàng