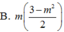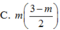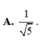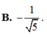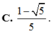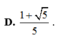Question

Biết sinα + cosα = \(\sqrt{2 }\) . Tính giá trị của sin⁴α + cos⁴α.

Mn giúp e câu này vớiiiii

 

Answer 1

\(sin\alpha+cos\alpha=\sqrt{2}\)

=>\(\left(sin\alpha+cos\alpha\right)^2=\left(\sqrt{2}\right)^2=2\)

=>\(1+2\cdot sin\alpha\cdot cos\alpha=2\)

=>\(2\cdot sin\alpha\cdot cos\alpha=1\)

=>\(sin\alpha\cdot cos\alpha=\dfrac{1}{2}\)

\(sin^4\alpha+cos^4\alpha=\left(sin^2\alpha+cos^2\alpha\right)^2-2\cdot sin^2\alpha\cdot cos^2\alpha\)

\(=1-2\cdot\left(sin\alpha\cdot cos\alpha\right)^2\)

\(=1-2\cdot\left(\dfrac{1}{2}\right)^2=1-\dfrac{2}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)