Bạn Mai dự định cắt một miếng bìa có dạng tam giác vuông với độ dài hai cạnh góc vuông lần lượt là 6(cm) và 8(cm). Sau khi xem xét lại, bạn Mai quyết định tăng độ dài cạnh góc vuông 6(cm) thêm x(cm) và tăng cạnh góc vuông 8(cm) thêm y(cm). (Hình vẽ bên).
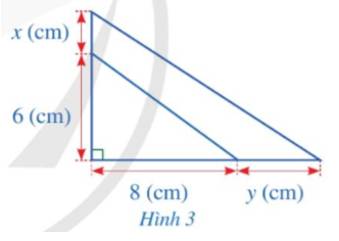
a) Viết đa thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y.
b) Tính diện tích phần tăng thêm khi x=2 và y=4
a) Đa thức biểu thị diện tích phần tăng thêm của miếng bìa là:
\(\dfrac{1}{2}\cdot\left(6+x\right)\cdot\left(8+y\right)-\dfrac{1}{2}\cdot6\cdot8\)
\(=\dfrac{1}{2}\cdot\left(48+6y+8x+xy\right)-3\cdot8\)
\(=24+3y+4x+\dfrac{xy}{2}-24\)
\(=3y+4x+\dfrac{xy}{2}\)
b) Phần diện tích tăng thêm là:
\(3\cdot4+4\cdot2+\dfrac{2\cdot4}{2}=24\left(cm^2\right)\)
a) Diện tích tam giác sau khi tăng thêm:
(6 + x).(8 + y) : 2
= (48 + 6y + 8x + xy) : 2
= 24 + 3y + 4x + xy/2
Diện tích phần tăng thêm:
24 + 3y + 4x + xy/2 - 6.8:2
= 4x + 3y + xy/2 (cm)²
b) Khi x = 2 và y = 4 thì diện tích phần tăng thêm là:
4.2 + 3.4 + 2.4/2
= 8 + 12 + 4
= 24 (cm²)
\(a,Diện.tích.tam.giác.vuông.mới:\dfrac{\left(6+x\right)\left(8+y\right)}{2}\left(cm^2\right)\\ Diện.tích.phần.tăng.thêm:\\ \dfrac{\left(6+x\right)\left(8+y\right)}{2}-\dfrac{xy}{2}=\dfrac{48+xy+8x+6y}{2}-\dfrac{6.8}{2}\\ =\dfrac{48+8x+6y}{2}+\dfrac{xy}{2}-24=4x+3y+\dfrac{xy}{2}\left(cm^2\right)\\ b,Diện.tích.tăng.thêm:4x+3y+\dfrac{xy}{2}=4.2+3.4+\dfrac{2.4}{2}=24\left(cm^2\right)\)















