`1)` Với `0 < a \ne 1` có:
`P=(1/[1-\sqrt{a}]-1/[1+\sqrt{a}])(1/\sqrt{a}+1)`
`P=[1+\sqrt{a}-1+\sqrt{a}]/[(1-\sqrt{a})(1+\sqrt{a})].[\sqrt{a}+1]/\sqrt{a}`
`P=[2\sqrt{a}]/[\sqrt{a}(1-\sqrt{a})]`
`P=2/[1-\sqrt{a}]`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`2)a=9+4\sqrt{2}` t/m đk
`=>\sqrt{a}=\sqrt{9+4\sqrt{2}}=\sqrt{(2\sqrt{2}+1)^2}=2\sqrt{2}+1`
Thay `\sqrt{a}=2\sqrt{2}+1` vào `P` có: `P=2/[1-2\sqrt{2}-1]=[-1]/\sqrt{2}=[-\sqrt{2}]/2`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`3)` Với `0 < a \ne 1` có:
`P > 1/2<=>2/[1-\sqrt{a}] > 1/2<=>2/[1-\sqrt{a}]-1/2 > 0`
`<=>[4-1+\sqrt{a}]/[2(1-\sqrt{a})] > 0`
`<=>[3+\sqrt{a}]/[1-\sqrt{a}] > 0` Mà `3+\sqrt{a} > 0`
`=>1-\sqrt{a} > 0<=>\sqrt{a} < 1<=>a < 1` Kết hợp đk
`=>0 < a < 1`
Bài 1:
a: \(P=\dfrac{1+\sqrt{a}-1+\sqrt{a}}{1-a}\cdot\dfrac{\sqrt{a}+1}{\sqrt{a}}=\dfrac{-2}{\sqrt{a}-1}\)
2: Khi \(a=9+4\sqrt{2}\) thì \(P=\dfrac{-2}{2\sqrt{2}+1-1}=\dfrac{-1}{\sqrt{2}}\)












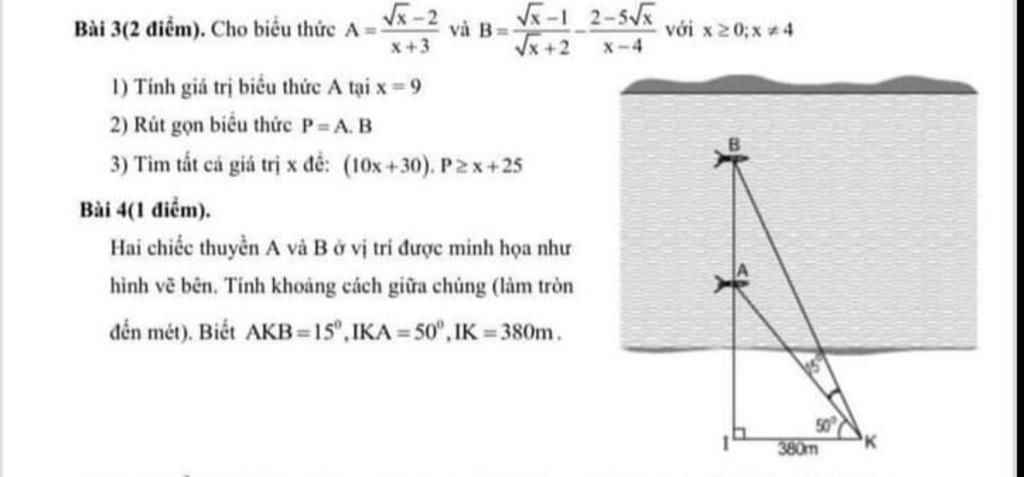








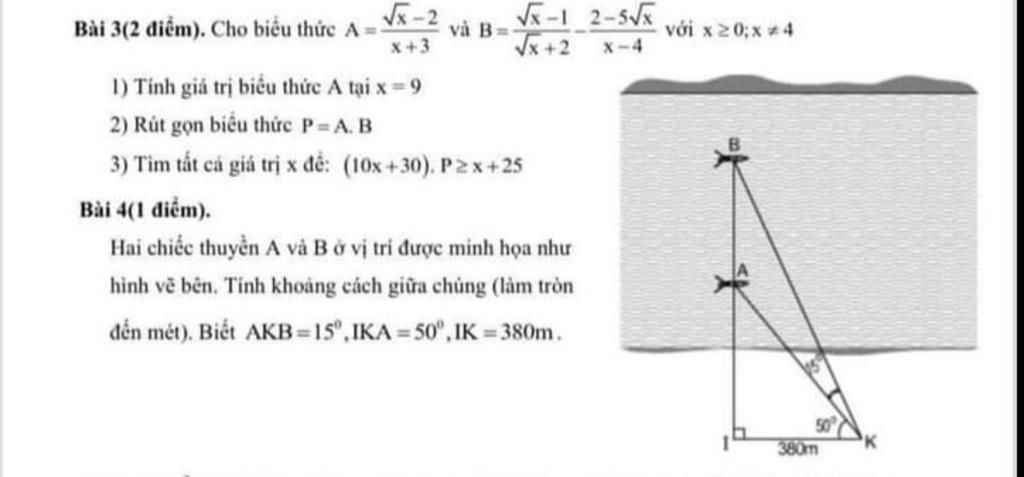
 bài 4 câu c thôi ạ
bài 4 câu c thôi ạ
 Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ