Question

Bài 1:  - Cho tam giác PQR đều .k ẻ BH vuông góc với QR. Tính độ dài các cạnh tam giác và diện tích tam giác PQR:  a. PH = 3 cm   b.PH = √3 cm

Bài 2: cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. Tính độ dài AH, BC,BH,CH:

a. AB=3cm , AC=4cm

b. AB=15cm , AC=20cm    

Answer 1

Bài 1 đã giải

2.

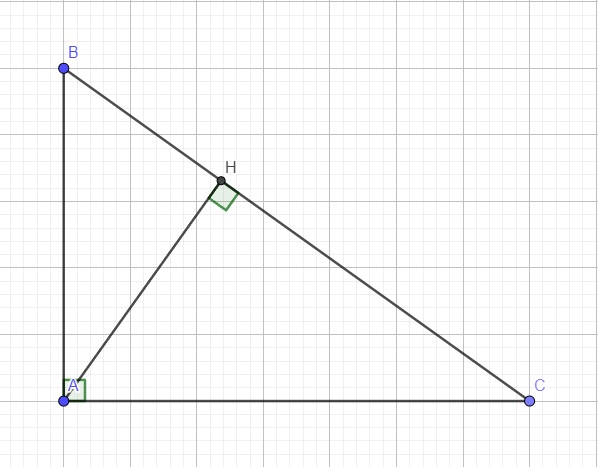
Do tam giác ABC vuông tại A nên: \(S_{\Delta ABC}=\dfrac{1}{2}AB.AC\) (1)

Mặt khác AH là đường cao ứng với BC nên ta cũng có: \(S_{\Delta ABC}=\dfrac{1}{2}AH.BC\) (2)

(1);(2) \(\Rightarrow\dfrac{1}{2}AB.AC=\dfrac{1}{2}AH.BC\)

\(\Rightarrow AH=\dfrac{AB.AC}{BC}\)

a.

Áp dụng định lý Pitago:

\(BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)

Theo cmt: \(AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}\left(cm\right)\)

Áp dụng Pitago cho tam giác vuông ABH:

\(BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-\left(\dfrac{12}{5}\right)^2}=\dfrac{9}{5}\left(cm\right)\)

\(CH=BC-BH=5-\dfrac{9}{5}=\dfrac{16}{5}\left(cm\right)\)

b.

Tương tự câu a:

\(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)

\(AH=\dfrac{15.20}{25}=12\left(cm\right)\)

\(BH=\sqrt{15^2-12^2}=9\left(cm\right)\)

\(CH=25-9=16\left(cm\right)\)

Answer 2