Các câu hỏi tương tự
Cho hàm số
f
(
x
)
x
2
+
1
x
3
-
x
+...
Đọc tiếp
Cho hàm số f ( x ) x 2 + 1 x 3 - x + 6 x ≢ 3 ; x ≢ 2 b + 3 x = 3 ; b ∈ R . Tìm b để f(x) liên tục tại x= 3.
A. 3
B. - 3
C. 2 3 3
D. - 2 3 3
Cho hàm số:
f
(
x
)
x
2
+
1
x
3
-
x
+...
Đọc tiếp
Cho hàm số: f ( x ) = x 2 + 1 x 3 - x + 6 x ≠ 3 ; x ≠ 2 b + 3 x = 3 ; b ∈ ℝ Tìm b để f(x) liên tục tại x = 3
![]()
![]()
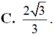
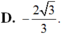
Chứng minh rằng với mọi số thực a, b, c phương trình:
(
x
–
a
)
.
(
x
-
b
)
+
(
x
-
b
)
.
(
x
-
c
)
+
(
x
–
c
)
.
(
x
-
a
)
0...
Đọc tiếp
Chứng minh rằng với mọi số thực a, b, c phương trình: ( x – a ) . ( x - b ) + ( x - b ) . ( x - c ) + ( x – c ) . ( x - a ) = 0 có ít nhất một nghiệm.
CMR: Biểu thức sau không phụ thuộc vào x: A=-sin⁴x +cos⁴x + 2sin²x B=sin⁴x + cos²x × sin²x + cos²x C= cos⁴x + cos²x × sin²x + cos²x
1) Cho \(a,b,c\) là các số thực dương. Xét tính đơn điệu của hàm số \(f\left(x\right)=\dfrac{a^x}{b^x+c^x}+\dfrac{b^x}{c^x+a^x}+\dfrac{c^x}{a^x+b^x}\) khi \(x>0\)
2) Chứng minh \(4^{\sin x}+2^{\tan x}>2^{\sqrt{3x+2}}\) với \(x\in\left(0;\dfrac{\pi}{2}\right)\)
a) lim\(\dfrac{x^2-1}{x+1}\)(x-->-3)
b) lim\(\dfrac{4-x^2}{x+2}\)(x-->-2)
a) tính gtrị của biểu thức A = \(\sqrt{3}+\sqrt{12}-\sqrt{27}-\sqrt{36}\)
b) cho bt B = \(\dfrac{2}{\sqrt{x-1}}-\dfrac{1}{\sqrt{x}}+\dfrac{3\sqrt{x-5}}{\sqrt{x\left(\sqrt{x-1}\right)}}\) với x > 0 và x \(\ne\) 1 . rút gọn bt và tìm x để B = 2
\(a,\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-\sqrt{x^2+x+1}}{x^2-2x+1}\)
\(b,\lim\limits_{x\rightarrow7}\dfrac{\sqrt{x-3}-2}{49-x^2}\)
Tìm các số thực a, b thoả mãn:
\(\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left[\left(a^3+b^3\right)x^2-\left(x+a^2b\right)\sqrt{x^2+2\left(ab\right)^2}\right]}{x-b-1}\)