Câu 2:
a: \(B=\dfrac{2\left(x+4\right)}{x-3\sqrt{x}-4}+\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{8}{\sqrt{x}-4}\)
\(=\dfrac{2\left(x+4\right)}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{8}{\sqrt{x}-4}\)
\(=\dfrac{2\left(x+4\right)+\sqrt{x}\left(\sqrt{x}-4\right)-8\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x+8+x-4\sqrt{x}-8\sqrt{x}-8}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+1\right)}=\dfrac{3x-12\sqrt{x}}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+1\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+1}\)
b: Để B là số nguyên thì \(3\sqrt{x}⋮\sqrt{x}+1\)
=>\(3\sqrt{x}+3-3⋮\sqrt{x}+1\)
=>\(-3⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1\in\left\{1;3\right\}\)
=>\(\sqrt{x}\in\left\{0;2\right\}\)
=>\(x\in\left\{0;4\right\}\)
1:
b: \(B=\dfrac{3}{2+\sqrt{3}}-\dfrac{13}{4-\sqrt{3}}+\dfrac{6}{\sqrt{3}}\)
\(=\dfrac{3\left(2-\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}-\dfrac{13\left(4+\sqrt{3}\right)}{16-3}+2\sqrt{3}\)
\(=6-3\sqrt{3}-4-\sqrt{3}+2\sqrt{3}=2-2\sqrt{3}\)
a: \(A=\sqrt{12}-\sqrt{27}-\sqrt{48}-\sqrt{108}\)
\(=2\sqrt{3}-3\sqrt{3}-4\sqrt{3}-6\sqrt{3}\)
\(=-11\sqrt{3}\)
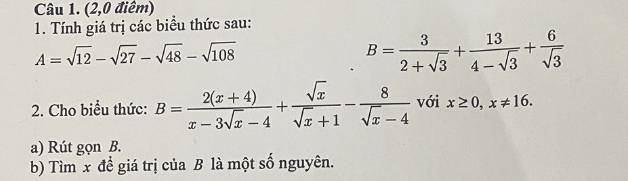
em nhờ các thầy cô gợi ý lời giải bài 17 và 18 giúp em ạ
