Lời giải:
a. $x=4-2\sqrt{3}=(\sqrt{3}-1)^2\Rightarrow \sqrt{x}=\sqrt{3}-1$
Khi đó:
$Q=\frac{\sqrt{3}-1+1}{\sqrt{3}-1-3}=\frac{-3-4\sqrt{3}}{13}$
b.
\(P=\frac{2\sqrt{x}(\sqrt{x}-3)+\sqrt{x}(\sqrt{x}+3)-(3x+3)}{(\sqrt{x}-3)(\sqrt{x}+3)}\\ =\frac{-3\sqrt{x}-3}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{-3(\sqrt{x}+1)}{(\sqrt{x}-3)(\sqrt{x}+3)}\)
\(M=\frac{P}{Q}=\frac{-3(\sqrt{x}+1)}{(\sqrt{x}-3)(\sqrt{x}+3)}:\frac{\sqrt{x}+1}{\sqrt{x}-3}=\frac{-3(\sqrt{x}+1)}{(\sqrt{x}-3)(\sqrt{x}+3)}.\frac{\sqrt{x}-3}{\sqrt{x}+1}=\frac{-3}{\sqrt{x}+3}\)
c.
\(A=xM+\frac{4x+7}{\sqrt{x}+3}=\frac{-3x}{\sqrt{x}+3}+\frac{4x+7}{\sqrt{x}+3}=\frac{x+7}{\sqrt{x}+3}\)
Áp dụng BĐT Cô-si:
$x+1\geq 2\sqrt{x}\Rightarrow x+7\geq 2\sqrt{x}+6=2(\sqrt{x}+3)$
$\Rightarrow A\geq \frac{2(\sqrt{x}+3)}{\sqrt{x}+3}=2$
Vậy $A_{\min}=2$. Giá trị này đạt tại $x=1$
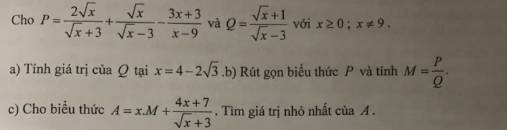
Anh chị giúp em với ạ^^
