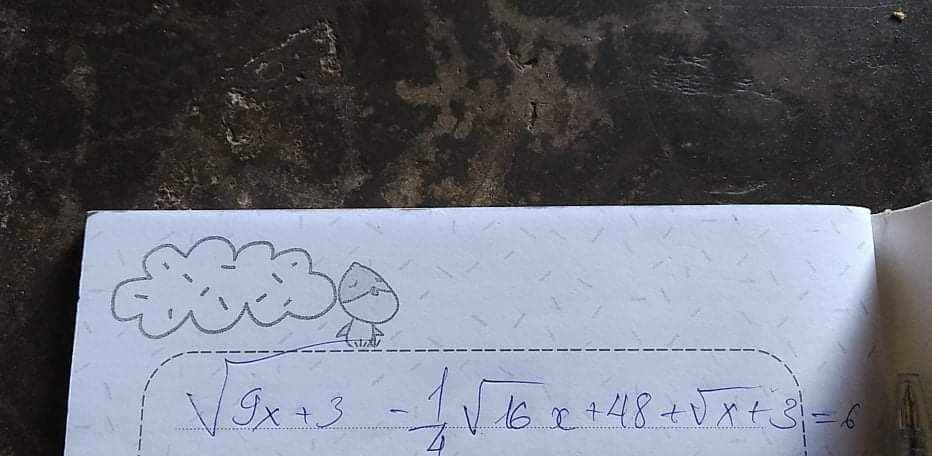a) ĐKXĐ\(\left\{{}\begin{matrix}30\ge\dfrac{5}{x^2}\\6x^2\ge\dfrac{5}{x^2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2\ge\dfrac{1}{6}\\x^4\ge\dfrac{5}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2\ge\dfrac{1}{6}\\x^2\ge\sqrt{\dfrac{5}{6}}\end{matrix}\right.\Leftrightarrow x^2\ge\sqrt{\dfrac{5}{6}}\)
Đặt 6x2=a; 5/x2=b (a≥b>0)
\(\Rightarrow ab=30\)
Khi đó phương trình trở thành:
\(\sqrt{ab-b}+\sqrt{a-b}=a\)
\(\Leftrightarrow\sqrt{ab-b}=a-\sqrt{a-b}\)
\(\Leftrightarrow ab-b=a^2-2a\sqrt{a-b}+a-b\)
\(\Leftrightarrow ab=a^2-2a\sqrt{a-b}+a\)
Vì \(a\ne0\) nên chia cả 2 vế cho a, ta được:
\(b=a-2\sqrt{a-b}+1\)
\(\Leftrightarrow a-b-2\sqrt{a-b}+1=0\)
\(\Leftrightarrow\left(\sqrt{a-b}-1\right)^2=0\)
\(\Leftrightarrow a-b=1\)
\(\Leftrightarrow6x^2-\dfrac{5}{x^2}=1\)
\(\Leftrightarrow6x^4-x^2-5=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(6x^2+5\right)=0\)
\(\Leftrightarrow x^2-1=0\left(6x^2+5>0\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(TM\right)\\x=-1\left(TM\right)\end{matrix}\right.\)
Vậy \(S=\left\{-1;1\right\}\)
Tick nha bạn 😘
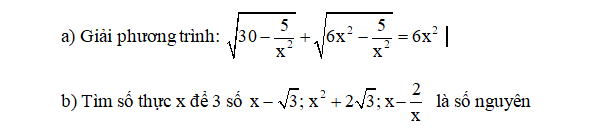
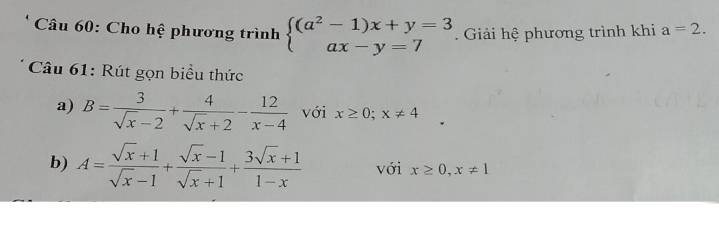
Anh chị giúp em với ạ^^
