Lời giải:
a. ĐKXĐ: $x\geq 0; x\neq 1$
\(P=\frac{x+2-\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+1}:\left[\frac{4-\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}-\frac{\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}+1)(\sqrt{x}-1)}\right]\)
\(=\frac{2-\sqrt{x}}{\sqrt{x}+1}:\frac{4-\sqrt{x}-(x-\sqrt{x})}{(\sqrt{x}-1)(\sqrt{x}+1)}\\ =\frac{2-\sqrt{x}}{\sqrt{x}+1}:\frac{4-x}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{2-\sqrt{x}}{\sqrt{x}+1}.\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{(2-\sqrt{x})(2+\sqrt{x})}\)
\(=\frac{\sqrt{x}-1}{2+\sqrt{x}}\)
b. $x=6-2\sqrt{5}=(\sqrt{5}-1)^2\Rightarrow \sqrt{x}=\sqrt{5}-1$
Khi đó:
$P=\frac{\sqrt{5}-2}{\sqrt{5}+1}=\frac{7-3\sqrt{5}}{4}$
c.
$P=\frac{1}{2}\Leftrightarrow \frac{\sqrt{x}-1}{\sqrt{x}+2}=\frac{1}{2}$
$\Leftrightarrow 2(\sqrt{x}-1)=\sqrt{x}+2$
$\Leftrightarrow \sqrt{x}=4$
$\Leftrightarrow x=16$
d.
$P-1=\frac{\sqrt{x}-1}{\sqrt{x}+2}-1=\frac{-3}{\sqrt{x}+2}<0$ do $-3<0$ và $\sqrt{x}+2\geq 2>0$ với mọi $x\in$ ĐKXĐ
$\Rightarrow P<1$
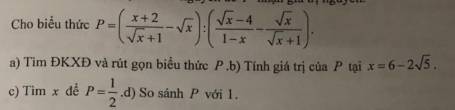
Anh chị giúp em với ạ^^
