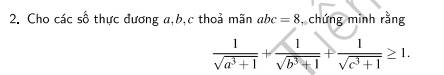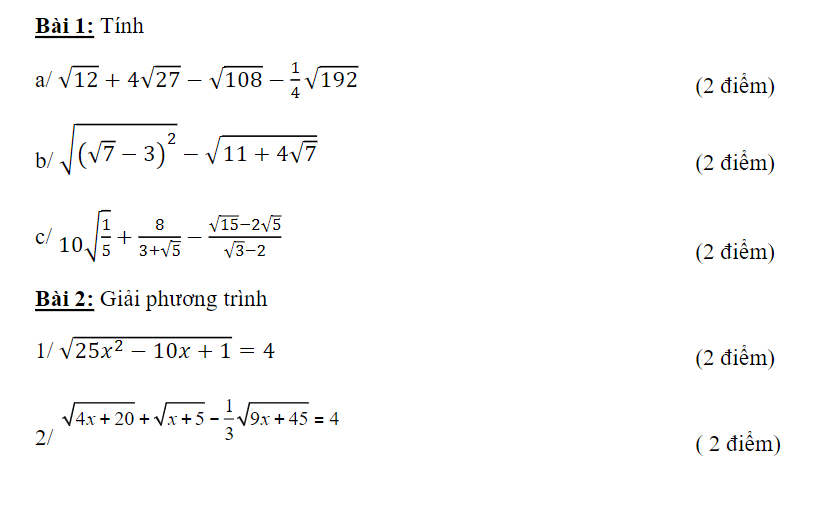Bài 2(hình 1)
\(\dfrac{\sqrt{x^2-4}}{\sqrt{x-2}}=3\)
<=> \(\dfrac{\sqrt{\left(x+2\right)\left(x-2\right)}}{\sqrt{x-2}}=\sqrt{x+2}\)
<=> \(\sqrt{x+2}=3\)
<=> x + 2 = \(\sqrt{3}\)
<=> x = \(\sqrt{3}-2\)
\(\dfrac{\sqrt{x^2-4}}{\sqrt{x-2}}=3\)
\(\dfrac{\sqrt{\left(x-2\right)^2}}{\sqrt{x-2}}=3\)
\(\dfrac{\sqrt{x-2}.\sqrt{x-2}}{\sqrt{x-2}}=3\)
\(\sqrt{x-2}=3\)
\(\left(\sqrt{x-2}\right)^2=3^2\)
\(x-2=9\)
x = 11
\(1,A=\left(\dfrac{1}{\sqrt{1+a}}+\sqrt{1-a}\right):\left(\dfrac{1}{\sqrt{1-a^2}}+1\right)\left(-1< a< 1\right)\\ A=\dfrac{1+\sqrt{1-a^2}}{\sqrt{1+a}}:\dfrac{1+\sqrt{1-a^2}}{\sqrt{1-a^2}}\\ A=\dfrac{1+\sqrt{1-a^2}}{\sqrt{1+a}}\cdot\dfrac{\sqrt{\left(1-a\right)\left(1+a\right)}}{1+\sqrt{1-a^2}}=\sqrt{1-a}\)
\(2,\dfrac{\sqrt{x^2-4}}{\sqrt{x-2}}=3\left(x\ge2;x\le-2\right)\\ \Leftrightarrow\sqrt{x+2}=3\\ \Leftrightarrow x+2=9\Leftrightarrow x=7\)
\(3,P=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}+1-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\left(x>0\right)\\ P=\dfrac{\sqrt{x}\left(x\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-2\sqrt{x}-1\\ P=\sqrt{x}\left(\sqrt{x}+1\right)-2\sqrt{x}\\ P=x+\sqrt{x}-2\sqrt{x}\\ P=x-\sqrt{x}=x-\sqrt{x}+\dfrac{1}{4}-\dfrac{1}{4}=\left(\sqrt{x}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{4}\)
Câu 3:
Ta có: \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
=1-a
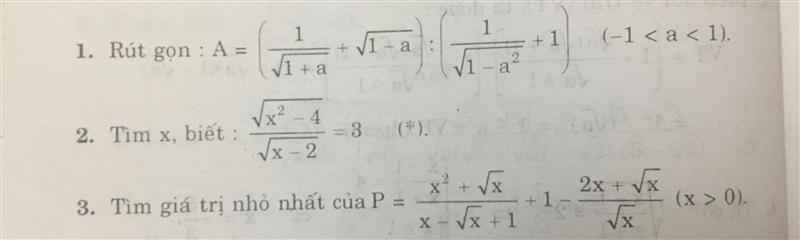
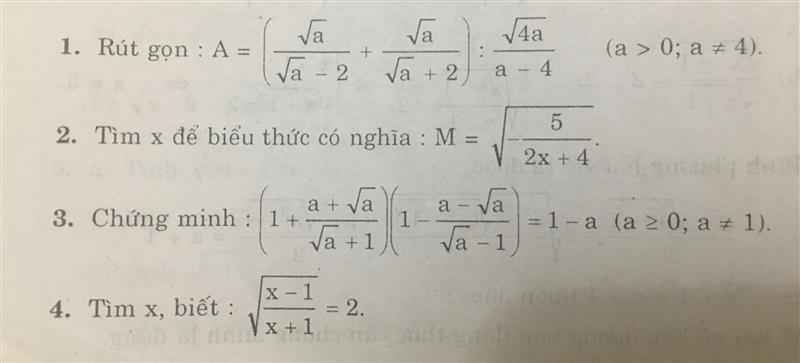
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 
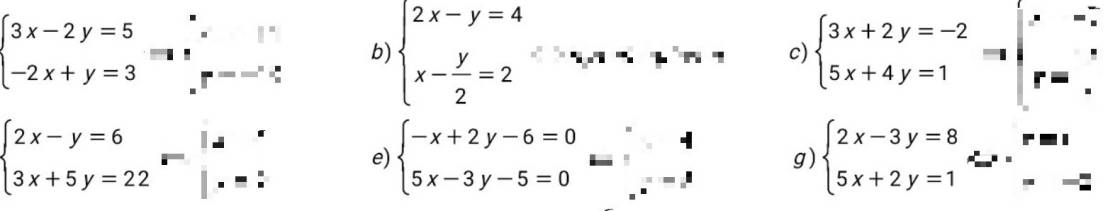
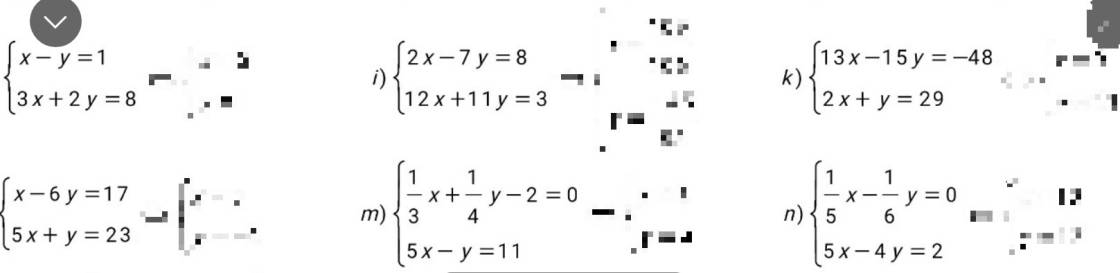giúp mik với mik đg cần gấp
