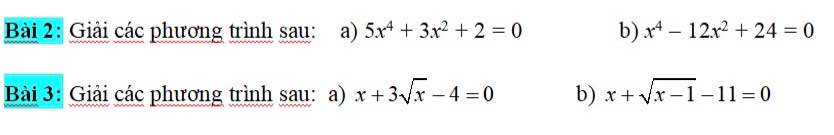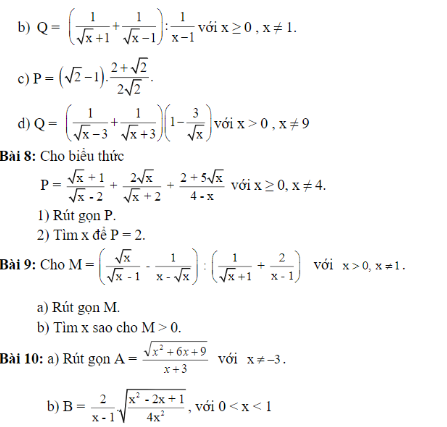Câu I.
2. Ta có:
\(\sqrt{a\left(1-b\right)\left(1-c\right)}\)
\(=\sqrt{a\left(1-b-c+bc\right)}\)
\(=\sqrt{a\left(a+2\sqrt{abc}+bc\right)}\) (vì \(a+b+c+2\sqrt{abc}=1\) nên \(a+2\sqrt{abc}=1-b-c\))
\(=\sqrt{a\left(\sqrt{a}+\sqrt{bc}\right)^2}\)
\(=\left|\sqrt{a}+\sqrt{bc}\right|\sqrt{a}\)
\(=\left(\sqrt{a}+\sqrt{bc}\right)\sqrt{a}\) (vì \(\sqrt{a}+\sqrt{bc}>0\))
\(=\sqrt{a^2}+\sqrt{abc}\)
\(=\left|a\right|+\sqrt{abc}\)
\(=a+\sqrt{abc}\) (vì \(a>0\))
Tương tự, ta cũng có:
\(\sqrt{b\left(1-c\right)\left(1-a\right)}=b+\sqrt{abc}\)
\(\sqrt{c\left(1-a\right)\left(1-b\right)}=c+\sqrt{abc}\)
Khi đó:
\(B=\sqrt{a\left(1-b\right)\left(1-c\right)}+\sqrt{b\left(1-c\right)\left(1-a\right)}+\sqrt{c\left(1-a\right)\left(1-b\right)}-\sqrt{abc}\)
\(=\left(a+\sqrt{abc}\right)+\left(b+\sqrt{abc}\right)+\left(c+\sqrt{abc}\right)-\sqrt{abc}\)
\(=a+\sqrt{abc}+b+\sqrt{abc}+c+\sqrt{abc}-\sqrt{abc}\)
\(=a+b+c+2\sqrt{abc}\)
\(=1\) (vì \(a+b+c+2\sqrt{abc}=1\))
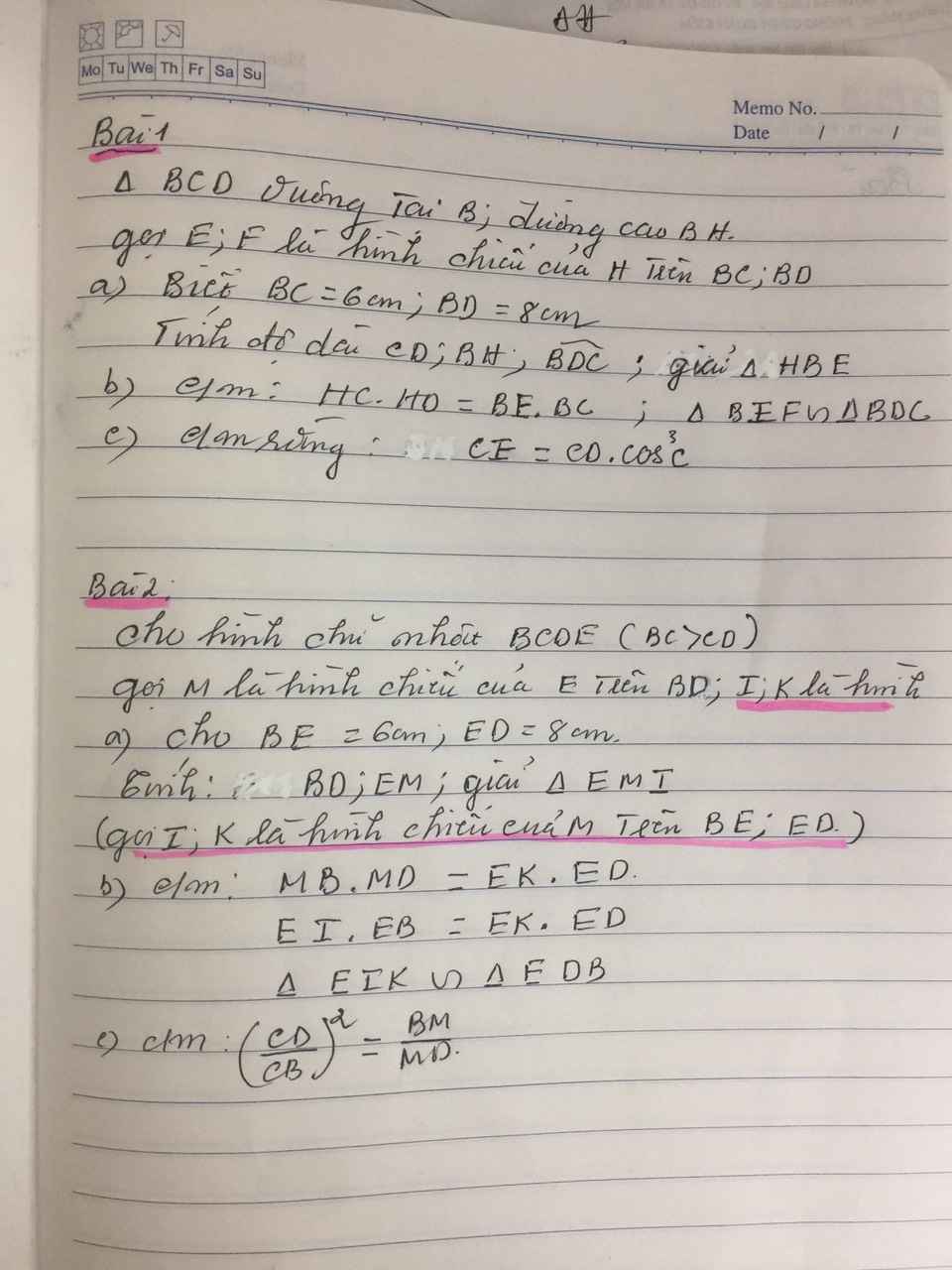
Cho 3 số dương a,b,c thỏa mãn a+b+c=1. CMR:
