5.Ta có số chính phương khi chi cho 8 có các số dư là 0,1,4
Mà 2 số đó là số lẻ => Mỗi số khia chia cho 8 sẽ dư 1 => Tổng 2 số chia 8 dư 2 => đpcm
Chứng minh tương tự, ta có hiệu 2 số chính phương đó khia cho 8 dư 1 - 1 = 0 => đpcm
6.Gọi số chính phương chẵn là (2k)^2 với k nguyên.
Khi đó (2k)^2 = 4k^2 chia hết cho 4 => đpcm
Gọi số chính phương lẻ là (2q + 1)^2 với q nguyên.
Khi đó, ta có (2q + 1)^2 = 4q^2 + 4q + 1 = 4q(q + 1) +1
Mà 4q(q + 1) chia hết cho 8 4q(q + 1) + 1 chia 8 dư 1 => đpcm
7.Gọi n là số nguyên. Khi đó n chia 3 sẽ có các khả năng về số dư là 0,1,2
Xét n = 3k + 1 (k nguyên) => n^2 = 9k^2 + 6k + 1 chia 3 dư 1
Xét n = 3k + 2 (k nguyên) => n^2 = 9k^2 + 12k + 4 chia 3 dư 1
Xét n = 3k (k nguyên) => n^2 = 9k^2 chia hết cho 3
=>đpcm
8.Gọi tổng của 3 số chình phương liên tiếp là (n - 1)^2 + n^2 + (n + 1)^2 ( n nguyên)
Khi đó, ta có (n - 1)^2 + n^2 + (n + 1)^2 = n^2 - 2n + 1 + n^2 + n^2 + 2n + 1 = 3n^2 + 2 chia 3 dư 2 => không phải là số chính phương (đpcm)
Gọi tổng của 4 số chính phương liên tiếp là (n - 2)^2 + (n - 1)^2 + n^2 + (n + 1)^2 (n nguyên)
Khi đó, ta có (n - 2)^2 + (n - 1)^2 + n^2 + (n + 1)^2 = n^2 - 4n + 4 + n^2 - 2n + 1 + n^2 + n^2 + 2n + 1 = 4n^2 - 4n + 6 chia 4 dư 2 => không phải là số chính phương (đpcm)
Gọi tổng 5 số chính phương liên tiếp là (n - 2)^2 + (n - 1)^2 + n^2 + (n + 1)^2 + (n + 2)^2 = n^2 - 4n + 4 + n^2 - 2n + 1 + n^2 + n^2 + 2n + 1 + n^2 + 4n + 4 = 5n^2 + 10 = 5(n^2 + 2) chia hết cho 5 nhưng không chia hết cho 25 (do n^2 chia 3 không dư 3) => không phải là số chính phương (đpcm)
9. \(A=2n^3+3n^2+n=n\left(2n^2+3n+1\right)=n\left[2n\left(n+1\right)+n+1\right]=n\left(n+1\right)\left(2n+1\right)\)*Vì \(n\left(n+1\right)⋮2\) nên \(A⋮2\) (1)
*Xét \(n=3k\Rightarrow A⋮3\)
Xét \(n=3k+1\Rightarrow2n+1=6k+3⋮3\Rightarrow A⋮3\)
Xét \(n=3k+2\Rightarrow n+1=3k+3⋮3\Rightarrow A⋮3\)
Vậy \(A⋮3\) (2)
Từ (1) và (2) ta suy ra đpcm.
\(A=a^3b-ab^3=ab\left(a^2-b^2\right)=ab\left(a+b\right)\left(a-b\right)\)
Chứng minh \(A⋮2\) :
Dễ dàng nhận thấy nếu a hoặc b chia hết cho 2 thì \(A⋮2\).
Nếu a,b đều lẻ thì \(a+b,a-b\) đều chia hết cho 2\(\Rightarrow A⋮2\)
Vậy \(A⋮2\forall a,b\in Z\).
Chứng minh \(A⋮3\)
Nếu 1 trong 2 số a,b có cùng số dư khi chia cho 3 thì \(A⋮3\).
Nếu a chia 3 dư 1, b chia 3 dư 2 hoặc ngược lại thì \(\left(a+b\right)⋮3\) \(\Rightarrow A⋮3\)
Vậy \(A⋮3\forall a,b\in Z\)
Từ 2 điều trên ta suy ra đpcm.
11. \(P=n^5-5n^3+4n=n\left(n^4-5n^2+4\right)=n\left[n^2\left(n^2-1\right)-4\left(n^2-1\right)\right]=n\left(n^2-1\right)\left(n^2-4\right)=\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)\)Vì đây là tích của 5 số nguyên liên tiếp nên: \(P⋮5\)
Do trong P có tích của 4 số nguyên liên tiếp nên: \(P⋮4\).
Do P có tích của 3 số nguyên liên tiếp nên \(P⋮6\)
Từ 3 điều trên suy ra \(P⋮120\)









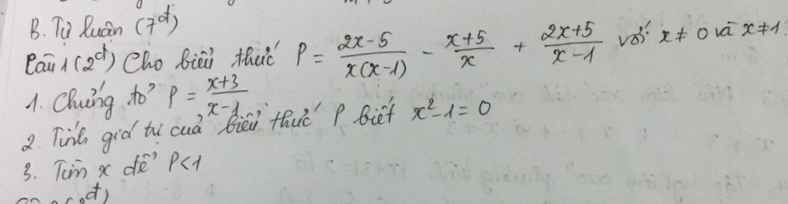 ai giúp mình với , mình đang cần gấp
ai giúp mình với , mình đang cần gấp


 ai giải giúp mình với ạ mình cảm ơn
ai giải giúp mình với ạ mình cảm ơn