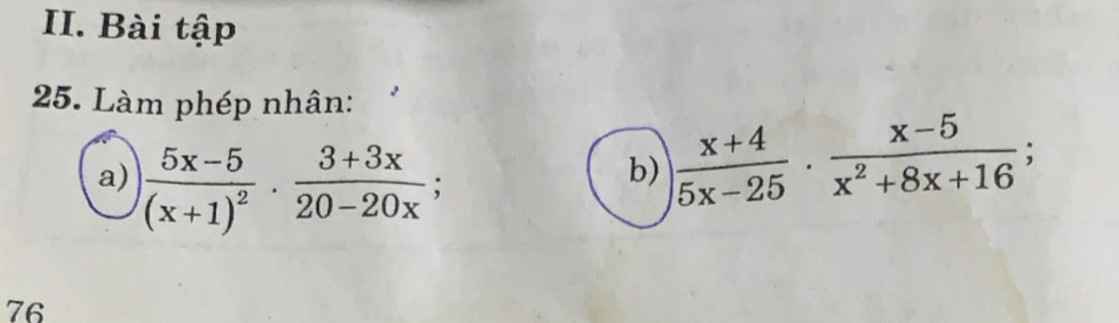1, Với x khác 0 ; x khác 1
\(P=\dfrac{2x-5-\left(x+5\right)\left(x-1\right)+2x^2+5x}{x\left(x-1\right)}\)
\(=\dfrac{2x-5-x^2-4x+5+2x^2+5x}{x\left(x-1\right)}=\dfrac{x^2+3x}{x\left(x-1\right)}=\dfrac{x+3}{x-1}\)
2, Ta có \(x^2=1\Leftrightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\x=1\left(ktm\right)\end{matrix}\right.\)
Thay vào ta được \(\dfrac{-1+3}{-1-1}=\dfrac{2}{-2}=-1\)
3, \(\dfrac{x+3}{x-1}-1< 0\Leftrightarrow\dfrac{x+3-x+1}{x-1}< 0\Rightarrow x-1< 0\Leftrightarrow x< 1\)
Kết hợp đk vậy x < 1 ; x khác 0

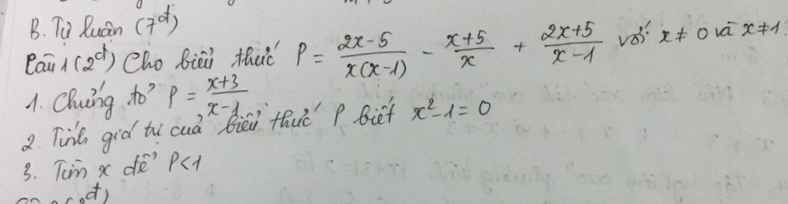 ai giúp mình với , mình đang cần gấp
ai giúp mình với , mình đang cần gấp