Dạng \(\sqrt{A}=B\)
Cách giải: pt tương đương với: \(\left\{{}\begin{matrix}B\ge0\\A=B^2\end{matrix}\right.\) (không cần tìm ĐKXĐ cho căn thức)
11.
\(\sqrt{x^2-x}=x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2-x=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x=0\end{matrix}\right.\) \(\Rightarrow x=0\)
12.
\(\sqrt{3-x^2}=x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\3-x^2=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2=\dfrac{3}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=\dfrac{\sqrt{6}}{2}\\x=-\dfrac{\sqrt{6}}{2}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow x=\dfrac{\sqrt{6}}{2}\)
13.
\(\sqrt{5-x^2}=x-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\5-x^2=\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\2x^2-2x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow x=2\)
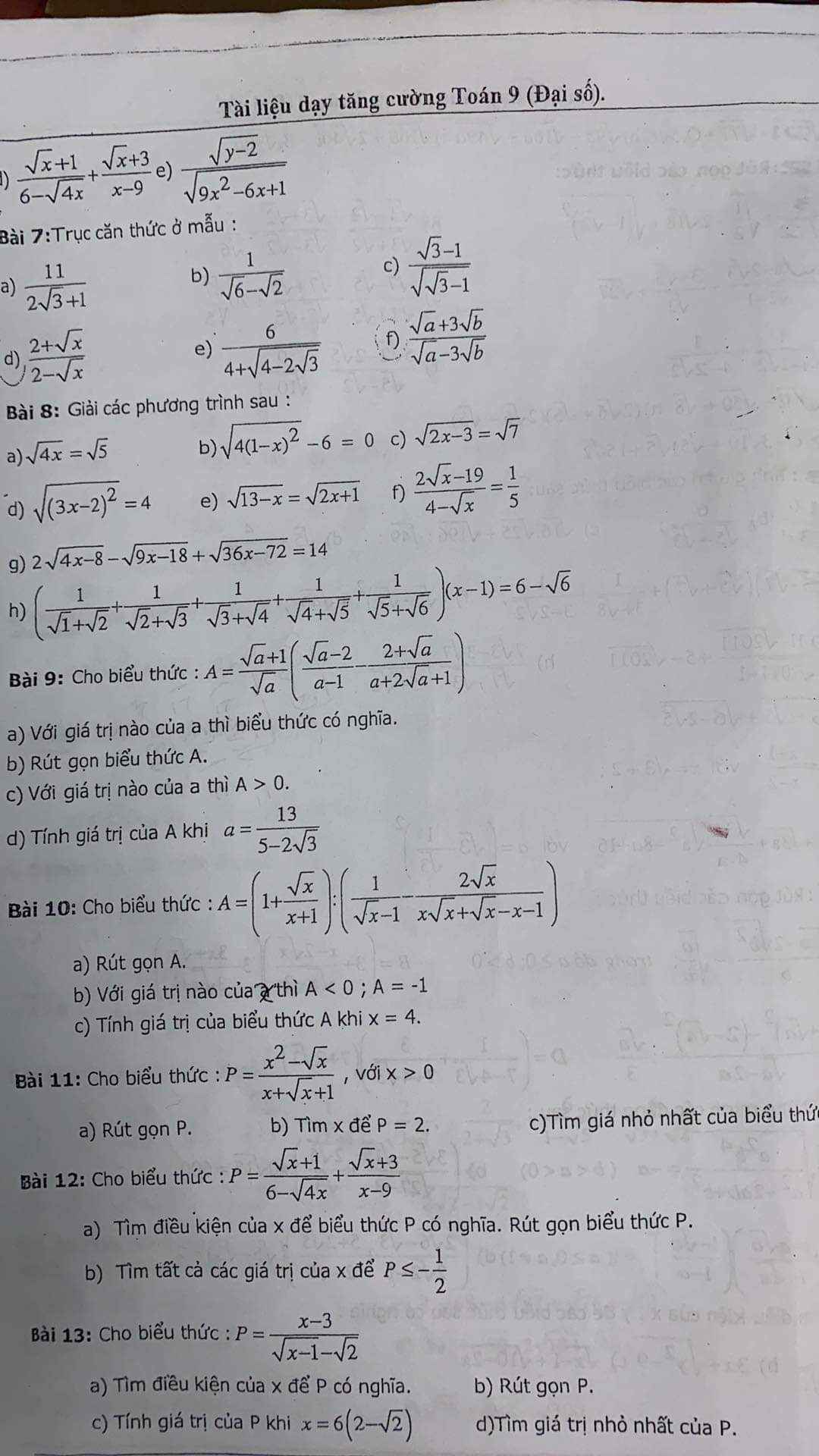
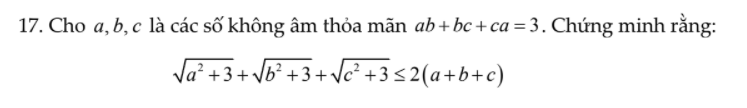câu này với ạ! Mình cảm ơn.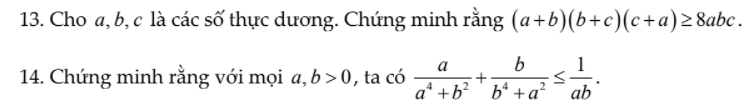
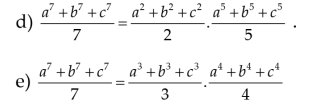ai giúp mình với mình cần gấp câu nào cũng được ạ
