Bài 4:
a. Khi $m=2$ thì hàm số là: $y=x+2$.
Cho $x=0$ thì $y=x+2=0+2=2$. Ta có điểm $(0,2)$
Cho $x=1$ thì $y=1+2=3$. Ta có điểm $(1,3)$
Nối $(0,2)$ với $(1,3)$ ta được đths $y=x+2$
b.
Để hàm đồng biến thì $m^2-3>0$
$\Leftrightarrow m> \sqrt{3}$ hoặc $m< -\sqrt{3}$
Để hàm nghịch biến thì $m^2-3<0$
$\Leftrightarrow -\sqrt{3}< m< \sqrt{3}$
c.
Để $(d)$ đi qua $A(1;2)$ thì:
$y_A=(m^2-3)x_A+2$
$\Leftrightarrow 2=(m^2-3).1+2=m^2-1$
$\Leftrightarrow m^2=3\Leftrightarrow m=\pm \sqrt{3}$
d. Để $(d)$ đi qua $B(1;8)$ thì:
$y_B=(m^2-3)x_B+2$
$\Leftrightarrow 8=(m^2-3).1+2=m^2-1$
$\Leftrightarrow m^2=9\Leftrightarrow m=\pm 3$
Bài 6:
$M$ nằm trên đường thẳng $2x+y=3$ nên:
$2x_M+y_M=3$
Mà $x_M=\frac{1}{2}$ nên $y_M=3-2x_M=3-2.\frac{1}{2}=2$
Vậy $M(\frac{1}{2};2)$
Gọi PTĐT $(d)$ là $y=ax+b$
$A(-2;1)\in (d)$ nên: $y_A=ax_A+b$
$\Rightarrow 1=-2a+b(1)$
$M(\frac{1}{2};2)\in (d)$ nên:
$y_M=ax_M+b$
$\Rightarrow 2=\frac{1}{2}a+b(2)$
Từ $(1); (2)\Rightarrow a=\frac{2}{5}; b=\frac{9}{5}$
$\Rightarrow (d): y=\frac{2}{5}x+\frac{9}{5}$
Bài 5:
a. $(d)$ cắt trục tung tại điểm có tung độ $2$, tức là cắt trục tung tại điểm $(0;2)$
$\Rightarrow 2=(m-1).0+m+1$
$\Leftrightarrow 2=m+1\Leftrightarrow m=1$
b. $d$ cắt trục hoành tại điểm có hoành độ $-3$, tức là cắt trục hoành tại điểm $(-3,0)$
$\Rightarrow 0=(m-1)(-3)+m+1$
$\Leftrightarrow 0=-3m+3+m+1$
$\Leftrightarrow 4-2m=0\Leftrightarrow m=2$
c.
Để $d$ tạo với trục hoành góc 45 độ thì:
$m-1=\tan 45^0$
$\Rightarrow m-1=1\Rightarrow m=2$






 Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ




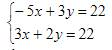 ai giúp em bài này với ạ 🥺 :)
ai giúp em bài này với ạ 🥺 :)


